Courbe de Lamé

Courbe de Lamé
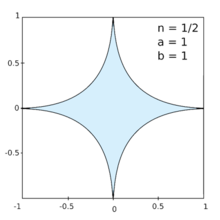
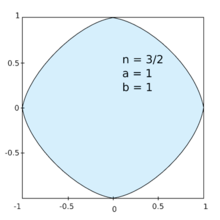
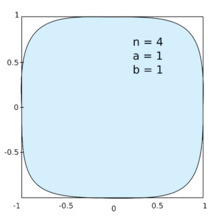
Exemples de courbes de Lamé
(n,a,b)=\left(\frac{1}{2}, 1, 1\right)
(n,a,b)=\left(\frac{3}{2}, 1, 1\right)
(n,a,b)=\left(4, 1, 1\right)

Les courbes de Lamé (ou superellipses) sont un groupe de courbes coniques définies pour la première fois par le mathématicien français Gabriel Lamé en 1818[1]. Elles sont définies par leur équation cartésienne:

\left|\frac{x}{a}\right|^n\! + \left|\frac{y}{b}\right|^n\! = 1

Propriétés

Les courbes de Lamé peuvent aussi être définies par l'équation paramétrique[2]:

\left. \begin{align} x\left(\theta\right) &= \plusmn a\cos^{\frac{2}{n}} \theta \\ y\left(\theta\right) &= \plusmn b\sin^{\frac{2}{n}} \theta \end{align} \right\} \qquad 0 \le \theta < \frac{\pi}{2}

L'aire \mathcal{A} de la surface délimitée par une courbe de Lamé est donnée[3] par:

\mathcal{A} = \frac{4^{\left(1-\frac{1}{n}\right)}ab\sqrt{\pi}\Gamma(1+\frac{1}{n})}{\Gamma(\frac{1}{2}+\frac{1}{n})}, où Γ est la fonction Gamma.

Références



Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Courbe de Lamé de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • courbe — [ kurb ] adj. et n. f. • 1699; corbe mil. XIIIe; lat. curvus 1 ♦ Adj. Qui change de direction sans former d angles; qui n est pas droit. ⇒ arqué, arrondi, bombé, busqué, cambré, cintré, circulaire, contourné, courbé, enroulé, galbé, incurvé,… …   Encyclopédie Universelle

  • courbé — courbe [ kurb ] adj. et n. f. • 1699; corbe mil. XIIIe; lat. curvus 1 ♦ Adj. Qui change de direction sans former d angles; qui n est pas droit. ⇒ arqué, arrondi, bombé, busqué, cambré, cintré, circulaire, contourné, courbé, enroulé, galbé,… …   Encyclopédie Universelle

  • Structure de la lame du sabre japonais — Afin d apprécier la lame d un sabre japonais, l amateur doit regarder certaines de ses caractéristiques en essayant d en omettre le moins possible. Ces indications peuvent lui permettre de retrouver certaines informations sur le forgeron (son… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • katana — [katana] n. m. ÉTYM. D. i.; mot japonais. ❖ ♦ Sabre des samouraïs japonais, légèrement courbe, à lame étroite, à dos épais, à un seul tranchant. || Poignée gainée de galuchat, garde (tsuba) ouvragée d un katana …   Encyclopédie Universelle

  • sabre — [ sabr ] n. m. • 1598; all. Sabel, var. de Säbel; hongr. száblya 1 ♦ Arme blanche, à pointe et à tranchant, à lame plus ou moins recourbée. ⇒ cimeterre, fam. coupe chou, épée, yatagan. Sabre de cavalerie (⇒vx latte) , d abordage, d infanterie.… …   Encyclopédie Universelle

  • Sabre — Pour les articles homonymes, voir Sabre (homonymie). Un sabre briquet Le sabre est une arme blanche d estoc et de taille, dont on utilise la pointe et le t …   Wikipédia en Français

  • INTERFÉRENCES LUMINEUSES — Lorsqu’on éclaire un plan matériel par deux sources ponctuelles, le phénomène observé ne résulte pas toujours de la superposition des intensités lumineuses émises par les deux sources. Si elles émettent des vibrations parallèles et… …   Encyclopédie Universelle

  • ACOUSTIQUE - Acoustique physiologique — Nous disons que nous entendons un son lorsque des vibrations de l’air ambiant, atteignant notre tympan, le mettent en mouvement dans des conditions d’amplitude et de fréquence telles que cette stimulation mécanique, qui est transmise par… …   Encyclopédie Universelle

  • COULEUR — Les radiations lumineuses perçues par notre œil se distinguent non seulement par leurs intensités, mais aussi par des caractéristiques qualitatives, leurs couleurs, qui n’ont d’abord été définies que par des comparaisons souvent grossières: les… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”