Conservation de la quantité de mouvement

Conservation de la quantité de mouvement

La conservation de la quantité de mouvement désigne, dans un référentiel inertiel, l'absence de variation de la quantité de mouvement du centre d'inertie d'un système dans certaines situations physiques : on parle alors d'un système isolé. Exemple : dans un référentiel inertiel, et en l'absence de frottement, un système de corps soumis à aucune force extérieure mais entrant en collision les uns avec les autres.

Mathématiquement, la quantité de mouvement \left( \vec {p} \right) est conservée lorsque sa variation instantanée est nulle :

\frac{d \vec p}{dt} = \vec 0

Ce principe est équivalent au principe d'inertie, mais fait intervenir la masse des corps (par définition \vec p = m . \vec v), ce qui permet d'introduire la notion de force (par définition \vec F = \frac{d\vec p}{dt} = m. \frac{d\vec v}{dt}) dans le cas où le mouvement n'est pas rectiligne uniforme.

Sommaire

Conditions

La quantité de mouvement du système reste la même alors que celles des masses prises individuellement varient.

Pour que la quantité de mouvement d'un système soit conservée, il est essentiel que la sommation des forces externes agissant sur le système soit nulle.

À l'inverse, les forces internes dues aux collisions n'empêchent pas la conservation. Il est cependant important de considérer le milieu comme un système car la quantité de mouvement de chaque corps prise individuellement n'est pas conservée[1]. C'est la somme vectorielle de chacune d'elles qui reste constante.

Collisions

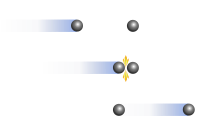
Avant une collision entre deux objets

La conservation de la quantité de mouvement peut intervenir lors d'une collision entre deux ou plusieurs objets ou particules. Lorsqu'il y a conservation, l'addition vectorielle des quantités de mouvement de chaque corps faisant partie du milieu conserve la même valeur avant et après la collision[2]. En ayant recours à ce principe, il n'est pas nécessaire de connaitre les forces qui ont lieu lors de la collision.

La quantité de mouvement se conserve dans trois types de collisions :

Les collisions élastiques

Après une collision élastique entre deux objets
Si une balle entre en collision élastique avec une autre balle de même masse initialement au repos, l'angle séparant leur deux trajectoire après la collision sera de 90°[3].

Une collision élastique est une collision qui prend place lorsque la somme des énergies cinétiques après la collision est égale à la somme des énergies cinétiques avant la collision. C'est une collision qui respecte le principe de conservation de l'énergie.

Les collisions inélastiques

Une collision inélastique est une collision qui prend place lorsque la somme des énergies cinétiques après la collision est différente de la somme des énergies cinétiques avant la collision. Ceci pourrait prendre place avec des balles de tennis. Une partie de l'énergie cinétique initiale sera transformée en énergie potentielle lors de la déformation de la balle, ce qui explique la variation négative de l'énergie cinétique du système[4].

Les collisions parfaitement inélastiques

Une collision parfaitement inélastique est une collision qui prend place lorsque le niveau d'énergie cinétique est plus bas que l'énergie cinétique qu'il y avait avant la collision. Durant cette collision, les deux objets s'unissent et se déplacent ensuite avec la même vitesse vectorielle. Par conséquent, on considère que les deux corps n'en forment plus qu'un à la suite de la collision[4].

Cas de non conservation

Quand la quantité de mouvement d'un système n'est pas conservée, la raison en est attribuée à des forces externes qui ne se compensent pas. En mécanique newtonienne, l'égalité suivante est la définition de la force influent sur le centre d'inertie du système :

\vec F = \frac{d \vec p}{dt}

Cette force s'appliquant sur le centre d'inertie est la résultante des diverses forces s'exerçant sur les corps du système.

En se basant sur cette relation, la variation de la quantité de mouvement \Delta \vec{p} peut être déterminée par la multiplication de la force moyenne exercée sur le système étudié par le temps d'action de cette force[5].

\Delta \vec{p} = \vec F_{moy}\Delta {t}

Exemples

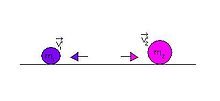
Choc entre deux boules de billard

Le choc entre deux boules de billard peut être approximé comme étant une collision élastique à une, deux ou trois dimensions.

Dans cet exemple, les équations de la conservation de la quantité de mouvement et de la conservation de l'énergie cinétique donnent, pour une particule de masse m1 et m2 ayant chacune une vitesse initiale \vec{u}_1 et \vec{u}_2 et une vitesse finale \vec{v}_1 et \vec{v}_2 :

m_1\vec{u}_1 + m_2\vec{u}_2 = m_1\vec{v}_1 + m_2\vec{v}_2
-m_1(\vec{v}_1 - \vec{u}_1) = m_2 (\vec{v}_2 - \vec{u}_2)

Notes et références

  1. ↑ Kane et Sternheim 1986, p. 163
  2. ↑ Kane et Sternheim 1986, p. 162
  3. ↑ Benson 2009, p. 275
  4. ↑ a et b Benson 2009, p. 264
  5. ↑ Benson 2009, p. 273

Sources bibliographiques

Ouvrage utilisé pour la rédaction de l'article : Ouvrage utilisé comme source pour la rédaction de cet article

  • Ouvrage utilisé pour la rédaction de l'articleHarris Benson (trad. Marc Séguin, Benoît Villeneuve, Bernard Marcheterre et Richard Gagnon), Physique 1 Mécanique, Édition du Renouveau Pédagogique, 2009, 4e éd., 465 p. 
  • Ouvrage utilisé pour la rédaction de l'articleJoseph W. Kane et Morton M. Sternheim, Physique, Interédition, 1986, 775 p. 

Voir aussi

Articles connexes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conservation de la quantité de mouvement de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • conservation de la quantité de mouvement — judesio kiekio momento tvermė statusas T sritis fizika atitikmenys: angl. conservation of angular momentum; conservation of moment of momentum vok. Drehimpulserhaltung, f; Erhaltung des Drehimpulses, f rus. сохранение момента количества движения …   Fizikos terminų žodynas

  • conservation de la quantité de mouvement — judesio kiekio tvermė statusas T sritis fizika atitikmenys: angl. linear momentum conservation; momentum conservation vok. Erhaltung der Bewegungsgröße, f; Impulserhaltung, f rus. сохранение импульса, n; сохранение количества движения, n pranc.… …   Fizikos terminų žodynas

  • loi de la conservation de la quantité de mouvement — judesio kiekio tvermės dėsnis statusas T sritis fizika atitikmenys: angl. momentum conservation law; principle of conservation of linear momentum; principle of conservation of momentum vok. Erhaltungssatz der Bewegungsgröße, m;… …   Fizikos terminų žodynas

  • conservation — [ kɔ̃sɛrvasjɔ̃ ] n. f. • fin XIIIe; lat. conservatio 1 ♦ Action de conserver, de maintenir intact ou dans le même état. ⇒ entretien, 1. garde, maintien, préservation, protection, 1. sauvegarde. Être chargé de la conservation d un monument.… …   Encyclopédie Universelle

  • Quantité conservée — Loi de conservation En physique, une loi de conservation exprime qu une propriété mesurable particulière d un système physique reste constante au cours de l évolution de ce système. Certaines lois de conservation n ont jamais été mises en… …   Wikipédia en Français

  • conservation du moment angulaire — judesio kiekio momento tvermė statusas T sritis fizika atitikmenys: angl. conservation of angular momentum; conservation of moment of momentum vok. Drehimpulserhaltung, f; Erhaltung des Drehimpulses, f rus. сохранение момента количества движения …   Fizikos terminų žodynas

  • conservation du moment cinétique — judesio kiekio momento tvermė statusas T sritis fizika atitikmenys: angl. conservation of angular momentum; conservation of moment of momentum vok. Drehimpulserhaltung, f; Erhaltung des Drehimpulses, f rus. сохранение момента количества движения …   Fizikos terminų žodynas

  • conservation of angular momentum — judesio kiekio momento tvermė statusas T sritis fizika atitikmenys: angl. conservation of angular momentum; conservation of moment of momentum vok. Drehimpulserhaltung, f; Erhaltung des Drehimpulses, f rus. сохранение момента количества движения …   Fizikos terminų žodynas

  • conservation of moment of momentum — judesio kiekio momento tvermė statusas T sritis fizika atitikmenys: angl. conservation of angular momentum; conservation of moment of momentum vok. Drehimpulserhaltung, f; Erhaltung des Drehimpulses, f rus. сохранение момента количества движения …   Fizikos terminų žodynas

  • conservation de l’impulsion — judesio kiekio tvermė statusas T sritis fizika atitikmenys: angl. linear momentum conservation; momentum conservation vok. Erhaltung der Bewegungsgröße, f; Impulserhaltung, f rus. сохранение импульса, n; сохранение количества движения, n pranc.… …   Fizikos terminų žodynas

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”