- 54-graphe de Ellingham-Horton
-
54-Graphe de Ellingham-Horton 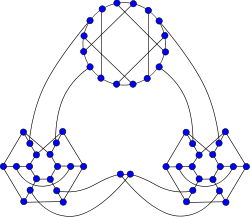
Représentation du 54-graphe de Ellingham-Horton.Nombre de sommets 54 Nombre d'arêtes 81 Distribution des degrés 3-régulier Rayon 9 Diamètre 10 Maille 6 Automorphismes 32 Nombre chromatique 2 Indice chromatique 3 Propriétés Cubique
Réguliermodifier 
Le 54-graphe de Ellingham-Horton est, en théorie des graphes, un graphe 3-régulier possédant 54 sommets et 81 arêtes. Il est construit comme contre-exemple à une conjecture de Tutte.
Sommaire
Histoire
En 1971, le mathématicien et cryptanalyste William Tutte conjecture qu'il n'existe pas de graphe 3-sommet-connexe qui soit cubique, bipartite et non-hamiltonien[1]. Mais J. D. Horton trouve un contre-exemple à 96 sommets, le graphe de Horton, publié par Bondy & Murty en 1976[2].
Après cela, d'autres contre-exemples sont découverts. En 1982, c'est un graphe à 92 sommets, encore construit par Horton (le 92-graphe de Horton)[3], puis, en 1983, Owens trouve un contre-exemple d'ordre 78[4].
Avec Ellingham, Horton publie deux contre-exemples à la conjecture de Tutte : un graphe d'ordre 78 en 1981 (le 78-graphe de Ellingham-Horton)[5] et un graphe d'ordre 54 en 1983 (le 54-graphe de Ellingham-Horton)[6]. A l'heure actuelle, ce graphe à 54 sommets est le plus petit graphe non-hamiltonien bipartite cubique 3-sommet-connexe connu.
Propriétés
Propriétés générales
Le diamètre du 54-graphe de Ellingham-Horton, l'excentricité maximale de ses sommets, est 10, son rayon, l'excentricité minimale de ses sommets, est 9 et sa maille, la longueur de son plus court cycle, est 6. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.
Coloriage
Le nombre chromatique du 54-graphe de Ellingham-Horton est 2. C'est-à-dire qu'il est possible de le colorer avec 2 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
L'indice chromatique du 54-graphe de Ellingham-Horton est 3. Il existe donc une 3-coloration des arêtes du graphe tels que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Voir aussi
Liens internes
Liens externes
Références
- (en) William Tutte, « On the 2-Factors of Bicubic Graphs », dans Discrete Mathematics, Elsevier, vol. 1, no 2, 22 mars 1971, p. 203-208 [lien DOI].
- (en) J. A. Bondy et U. S. R. Murty, Graph Theory with Applications, New York, North Holland, 1976, 1976e éd. (ISBN 978-0-444-19451-0) [lire en ligne], p. 240
- (en) J. D. Horton, « On two-factors of bipartite regular graphs », dans Discrete Mathematics, vol. 41, no 1, 1982, p. 35–41 [lien DOI].
- (en) P. J. Owens, « Bipartite cubic graphs and a shortness exponent », dans Discrete Mathematics, vol. 44, no 3, 1983, p. 327–330 [lien DOI].
- (en) M. N. Ellingham, Non-Hamiltonian 3-connected cubic partite graphs, Dept. of Math., Univ. Melbourne, 1981.
- (en) M. N. Ellingham, « Non-Hamiltonian 3-connected cubic bipartite graphs », dans Journal of Combinatorial Theory, Series B, vol. 34, no 3, 1983, p. 350–353 [lien DOI].
Catégorie :- Graphe remarquable
Wikimedia Foundation. 2010.
