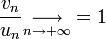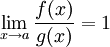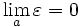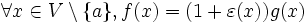Équivalent (mathématiques)

Équivalent

Pour les articles homonymes, voir équivalence.

La notion d'équivalence permet de dire précisément et « mathématiquement » quand deux fonctions ou deux suites ont le même comportement au voisinage d'un point ou de l'infini.

Une fois cet outil connu, se pose le problème du calcul des équivalents qui est d'une grande aide pour le calcul des développements asymptotiques, dont un cas particulier est le calcul des développements limités.

Pour bien s'en sortir dans ce travail, il faut bien savoir quelles opérations sur les équivalents sont permises et quelles autres sont interdites.

L'équivalence pour les suites

Définition

Soient $u n$ et $v n$ deux suites à valeurs dans un même espace vectoriel normé $E$ ou, si l'on veut, pour être moins général, dans un corps $\mathbb{K}$ ( $\mathbb{R}$ ou $\mathbb{C}$ ), c'est d'ailleurs ce cas, le moins général, qui est le plus courant et le plus utile.

On dit que $u n$ et $v n$ sont équivalentes si et seulement si, $u n - v n$ est négligeable devant $v n$ , ou, ce qui revient au même, $v n - u n$ négligeable devant $u n$ .

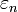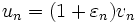Une définition équivalente peut être : il existe une suite $\varepsilon_n$ à valeurs dans $\mathbb{K}$ , qui tende vers zéro et vérifie $u_n=(1+\varepsilon_n)v_n$ .

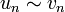On note alors $u_n\sim v_n$ .

Cas particulier plus simple

Dans le cas particulier où la suite $u n$ ne s'annule pas à partir d'un certain rang, les suites $u n$ et $v n$ sont équivalentes si, et seulement si,

$\frac{v_n}{u_n}\underset{n \rightarrow +\infty}{\longrightarrow}=1$

Autre formulation

On peut formuler les choses autrement : deux suites $u n$ et $v n$ sont équivalentes si, et seulement si, on a $u n = v n + o (v n)$ (en utilisant la notation petit "o").

Propriétés

La relation "être équivalent à" est une relation d'équivalence.
Si $u n$ converge vers 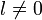$l\neq 0$ , alors, elle est équivalente à la suite constante égale à $l$ .

Opérations sur les équivalents

Article détaillé : Opérations sur les équivalents.

En général, les opérations de multiplication par une autre suite ou un scalaire, d'inversion, de division sont compatibles avec la relation "être équivalent à". Cependant, l'addition et la composition par des fonctions posent des problèmes.

Exemples

Un équivalent de la somme partielle $H n$ d'ordre n de la série harmonique est $H n ˜ln(n)$ .
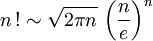Un équivalent célèbre est la formule de Stirling : $n\,!\sim \sqrt{2\pi n}\,\left({n \over e}\right)^n$ .
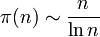Soit $π$ la suite dont le n-ième terme est égal au nombre de nombres premiers inférieurs ou égaux à $n$ . Le théorème des nombres premiers, qui est un résultat difficile, affirme que $\pi(n) \sim \frac{n}{\ln n}$ .

L'équivalence pour les fonctions

Définition élémentaire

Soient $I$ une partie de $\mathbb{R}$ , $a$ un point de l'adhérence de $I$ , $f$ et $g$ des applications de $I$ vers $\mathbb{R}$ , $g$ non nulle au voisinage de $a$ .

On dit que $f$ est équivalent à $g$ au voisinage de $a$ si et seulement si

$\lim_{x \to a} \frac{f(x)}{g(x)} = 1$

On écrit alors 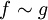$f\sim g$ qui se lit « $f$ est équivalent à $g$ ». S'il y a une ambiguïté sur le point a qu'on considère, on utilise la notation plus précise :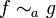 $f\sim_a g$

Définition plus savante

Soit $X$ un espace topologique, soit $A$ une sous-partie de $X$ . Soit 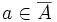$a \in \overline{A}$ un élément de $X$ adhérent à $A$ . Cet espace est l'espace de départ des fonctions qu'on va étudier. En quelque sorte, c'est l'espace des paramètres.

Soit 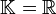$\mathbb{K}=\mathbb{R}$ ou $\mathbb{C}$ , muni de sa valeur absolue usuelle. Soit $E$ un $\mathbb{K}$ -espace vectoriel normé, appelé à être l'espace des valeurs de nos fonctions.

Soient $f$ et $g$ deux fonctions de $A$ dans $E$ .

On dit que $f$ et $g$ sont équivalentes en $a$ et on note 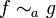$f\sim_a g$ si et seulement si, il existe un voisinage $V$ de $a$ dans 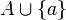$A \cup \{ a\}$ et une fonction $\varepsilon$ définie sur $V$ tels que :

$\lim_a \varepsilon = 0$
$\forall x\in V\setminus \{a\}, f(x)=(1+\varepsilon(x))g(x)$

Remarques

Si on veut être encore plus complet, on peut se placer dans le cadre des corps valués ou des espaces vectoriels topologiques au-dessus d'un corps valué.
La définition précédente est plus naturelle et s'exprime mieux dans le cadre des espaces de germes de fonctions.

Propriétés

La relation 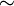$\sim$ est une relation d'équivalence.

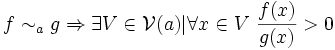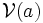$f \sim_a g \Rightarrow \exists V \in \mathcal{V}(a) | \forall x \in V\ \frac{f(x)}{g(x)} > 0$ , où $\mathcal{V}(a)$ représente l'ensemble des voisinages de a.

En particulier, f et g ont même signe localement autour de a.

Si 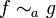$f \sim_a g$ et que 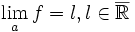$\lim_{a}f = l, l \in \overline {\mathbb R}$ , alors 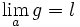$\lim_{a}g=l$ : deux fonctions équivalentes en a y ont la même limite.

Opérations sur les équivalents

Article détaillé : Opérations sur les équivalents.

Voir aussi

Négligeable

Portail des mathématiques

Ce document provient de « %C3%89quivalent ».

Catégorie : Analyse réelle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équivalent (mathématiques) de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Mathematiques en Egypte antique — Mathématiques dans l Égypte antique Cet article fait partie de la série Sciences dans l Égypte antique Mathématiques Géométrie Unités de mesure Chiffres Fraction … Wikipédia en Français
Mathématiques En Égypte Antique — Mathématiques dans l Égypte antique Cet article fait partie de la série Sciences dans l Égypte antique Mathématiques Géométrie Unités de mesure Chiffres Fraction … Wikipédia en Français
Mathématiques en Égypte antique — Mathématiques dans l Égypte antique Cet article fait partie de la série Sciences dans l Égypte antique Mathématiques Géométrie Unités de mesure Chiffres Fraction … Wikipédia en Français
Mathématiques en égypte antique — Mathématiques dans l Égypte antique Cet article fait partie de la série Sciences dans l Égypte antique Mathématiques Géométrie Unités de mesure Chiffres Fraction … Wikipédia en Français
Mathematiques a rebours — Mathématiques à rebours Les mathématiques à rebours sont une branche des mathématiques qui pourrait être définie simplement par l idée de “remonter aux axiomes à partir des théorèmes”, contrairement au sens habituel (des axiomes vers les… … Wikipédia en Français
Mathématiques renversées — Mathématiques à rebours Les mathématiques à rebours sont une branche des mathématiques qui pourrait être définie simplement par l idée de “remonter aux axiomes à partir des théorèmes”, contrairement au sens habituel (des axiomes vers les… … Wikipédia en Français
Mathématiques À Rebours — Les mathématiques à rebours sont une branche des mathématiques qui pourrait être définie simplement par l idée de “remonter aux axiomes à partir des théorèmes”, contrairement au sens habituel (des axiomes vers les théorèmes). Un peu plus… … Wikipédia en Français
Equivalent — Équivalent Pour les articles homonymes, voir équivalence. La notion d équivalence permet de dire précisément et « mathématiquement » quand deux fonctions ou deux suites ont le même comportement au voisinage d un point ou de l infini.… … Wikipédia en Français
Équivalent simple — Équivalent Pour les articles homonymes, voir équivalence. La notion d équivalence permet de dire précisément et « mathématiquement » quand deux fonctions ou deux suites ont le même comportement au voisinage d un point ou de l infini.… … Wikipédia en Français
Mathématiques en Mésopotamie — Mathématiques babyloniennes Photographie de la tablette YBC 7289 annotée. Les nombres écrits dans le système babylonien donnent la racine carrée de 2 avec quatre chiffres sexagésimaux significatifs, soit près de six chiffres décimaux : 1 +… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Équivalent (mathématiques)

Équivalent

Sommaire