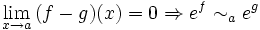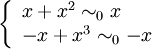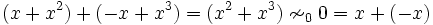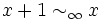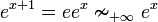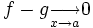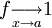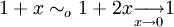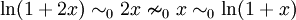Operations sur les equivalents

Operations sur les equivalents

Opérations sur les équivalents

Dans cet article, on fait le point sur les opérations qu'on a le droit d'effectuer sur les équivalents en analyse mathématique.

Sommaire

Règles simples

Inversion

Soient f,g deux fonctions qui, localement, sont non-nulles au voisinage de a (sauf peut-être en a). En particulier, on peut définir leurs inverses. Alors :

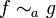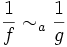Si f\sim_a g, on a \frac{1}{f}\sim_a\frac{1}{g}.


Démonstration

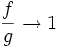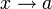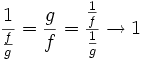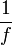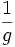Tout simplement, on sait qu'on a \frac{f}{g}\to 1 quand x \to a. Tenant compte des opérations sur les limites autorisées, on a donc \frac{1}{\frac{f}{g}}=\frac{g}{f}=\frac{\frac{1}{f}}{\frac{1}{g}}\to 1, et donc \frac{1}{f} et \frac{1}{g} qui sont équivalentes en a.

Produit

Soient les fonctions 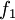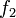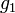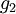f_1\,, f_2\,, g_1\,, g_2\,. On a alors :

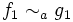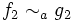Si f_1 \sim_a g_1 et f_2 \sim_a g_2 alors f1f2˜ag1g2.


Démonstration

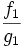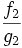On fait la démonstration dans le cas plus simple où on peut caractériser l'équivalence par la limite du quotient. On a ainsi : \frac{f_1}{g_1} et \frac{f_2}{g_2} tendent vers 1 quand 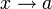x\to a et il en est donc de même pour leur produit . C'est-à-dire : 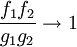\frac{f_1 f_2}{g_1 g_2}\to 1. Cela signifie bien que f1g1 et f2g2 sont équivalentes.

Multiplication par un scalaire

Soient les fonctions f,g et 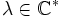\lambda \in \mathbb{C}^*. On a alors :

Si 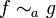f \sim_a g alors λf˜aλg.


Démonstration

C'est un cas particulier de la règle sur le produit des équivalents avec (f1,g1) = (f,g) et les fonctions f2,g2 constantes égales à λ.

Quotient

Soient les fonctions 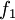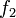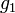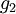f_1\,, f_2\,, g_1\,, g_2\,. On suppose que f2 et g2 ne s'annulent pas localement autour de a. On a alors:

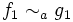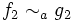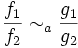Si f_1 \sim_a g_1 et f_2 \sim_a g_2 alors \frac{f_1}{f_2} \sim_a \frac{g_1}{g_2}.


Démonstration

D'après la règle sur l'inversion, on a 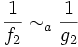\frac{1}{f_2}\sim_a \frac{1}{g_2}. On applique ensuite la règle sur le produit.

Puissance

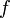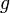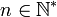Soient les fonctions f \,\!, g \,\! et n \in \mathbb{N}^*. On a alors :

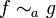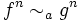Si f \sim_a g alors f^{n} \sim_a g^{n} \,\!.


Démonstration

C'est un cas particulier de la règle sur le produit des équivalents. 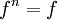f^n=f \,\!×...×f, n fois.

Règles plus subtiles

Composition

Il n'existe pas de théorème général. Cependant, on peut remarquer certains cas particuliers:

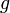  • Soient f\, et g\, deux fonctions définies sur un voisinage V de a (sauf peut-être en a):
\lim_{x \to a}{(f-g)(x)}=0 \Rightarrow e^f \sim_a e^g


démonstration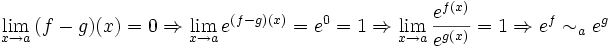

\lim_{x \to a}{(f-g)(x)}=0 \Rightarrow \lim_{x \to a}{e^{(f-g)(x)}} = e^0 = 1 \Rightarrow \lim_{x \to a}{\frac{e^{f(x)}}{e^{g(x)}}} = 1 \Rightarrow e^f \sim_a e^g\,

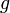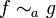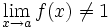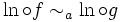  • Soient f\, et g\, deux fonctions définies sur un voisinage V de a (sauf peut-être en a), strictement positives sur V, telles que f \sim_a g et \lim_{x \to a} f(x) \ne 1. Alors on a: \ln \circ f \sim_a \ln \circ g.


démonstration

On a:
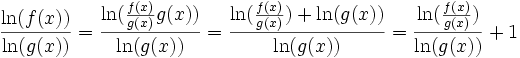
\frac{\ln(f(x))}{\ln(g(x))} = \frac{\ln(\frac{f(x)}{g(x)}g(x))}{\ln(g(x))} = \frac{\ln(\frac{f(x)}{g(x)})+\ln(g(x))}{\ln(g(x))} = \frac{\ln(\frac{f(x)}{g(x)})}{\ln(g(x))}+1
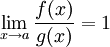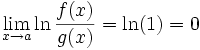
De plus, \lim_{x \to a}\frac{f(x)}{g(x)} = 1 donc \lim_{x \to a}{\ln \frac{f(x)}{g(x)}} = \ln(1) = 0
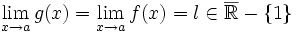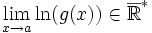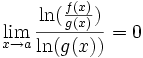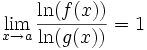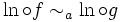
Or \lim_{x \to a}g(x) = \lim_{x \to a}f(x) = l \in \overline{\mathbb R}-\{1\} donc \lim_{x \to a}\ln(g(x)) \in \overline{\mathbb R}^* donc \lim_{x \to a}\frac{\ln(\frac{f(x)}{g(x)})}{\ln(g(x))} = 0\, donc \lim_{x \to a}\frac{\ln(f(x))}{\ln(g(x))} = 1 donc \ln \circ f \sim_a \ln \circ g

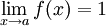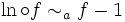
Remarque: si \lim_{x \to a}f(x) = 1 alors \ln \circ f \sim_a f - 1


démonstration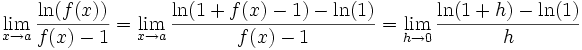

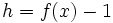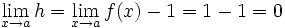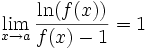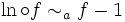\lim_{x \to a}\frac{\ln(f(x))}{f(x) - 1} = \lim_{x \to a}\frac{\ln(1+f(x)-1) - \ln(1)}{f(x)-1} = \lim_{h \to 0}\frac{\ln(1+h)-\ln(1)}{h} avec h = f(x)-1\,. Remarquons que \lim_{x \to a}h = \lim_{x \to a}f(x) - 1 = 1 - 1 = 0. On reconnaît la dérivée du logarithme en 1, qui vaut 1. Donc \lim_{x \to a}\frac{\ln(f(x))}{f(x)-1} = 1 donc \ln \circ f \sim_a f - 1.

Opérations interdites, contre-exemples

Somme, différence

Dans le cas général, on ne peut pas faire la somme ou la différence de fonctions équivalentes; il faut donc repasser par la limite du quotient. Par exemple, on a pour un x réel:

\left\{\begin{array}{l}x+x^2\sim_0x \\ -x+x^3\sim_0 -x \end{array} \right.

mais

(x+x^2)+(-x+x^3)=(x^2+x^3)\nsim_0 0=x+(-x)

Composition de fonctions

Exponentielle

Si 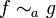f \sim_a g, on ne peut pas en déduire ef˜aeg. Par exemple

x+1 \sim_\infty x

mais

e^{x+1}=ee^x \nsim_{+\infty} e^x

L'hypothèse

f-g \underset{x \to a}{\longrightarrow} 0

est indispensable (voir le théorème énoncé plus haut).

Logarithme

Si 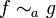f \sim_a g et que

f \underset{x \to a}{\longrightarrow} 1

on ne peut conclure 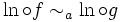\ln \circ f \sim_a \ln \circ g. Par exemple

1+x \sim_o 1+2x \underset{x \to 0}{\longrightarrow} 1

Or d'après un développement limité

ln(1 + x)˜0x

on a donc

\ln(1+2x)\sim_0 2x \nsim_0 x \sim_0 \ln(1+x)

L'hypothèse que f ne tende pas vers 1 est indispensable (voir théorème plus haut).

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Op%C3%A9rations sur les %C3%A9quivalents ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Operations sur les equivalents de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Opérations sur les équivalents — Dans cet article, on fait le point sur les opérations valides sur les équivalents de fonctions, en analyse mathématique. Sommaire 1 Règles simples 1.1 Inversion 1.2 Produit 1.3 …   Wikipédia en Français

  • Équivalents — Équivalent Pour les articles homonymes, voir équivalence. La notion d équivalence permet de dire précisément et « mathématiquement » quand deux fonctions ou deux suites ont le même comportement au voisinage d un point ou de l infini.… …   Wikipédia en Français

  • Les Mercedes Unimog — Unimog Unimog U400, version construite depuis 2000 Unimog est une marque commerciale de Mercedes Benz, créée pour promouvoir ses petits camions utilitaires tout terrain. Le nom est la contraction de l expression allemande UNIversal MOtor Gerät ,… …   Wikipédia en Français

  • Special Operations Executive — Sommaire 1 Présentation générale 1.1 Opérations 1.1.1 Objectifs des opérations 1.1.2 Techniques utilisées pour les o …   Wikipédia en Français

  • Nouveau cadre de la lutte anti-blanchiment dans les établissements financiers — Sommaire 1 Les personnes assujetties 2 L approche par les risques 2.1 La vigilance simplifiée 2.2 La vigilance normale …   Wikipédia en Français

  • INDE - Les sciences — L’histoire des sciences, au sens où nous l’entendons en Occident, a bénéficié d’apports spécifiques de l’Inde, au moins dans trois domaines: l’astronomie, les mathématiques et les sciences médicales. D’autres disciplines scientifiques, la… …   Encyclopédie Universelle

  • ISLAM - Les mathématiques et les autres sciences — «Et vous avez en ma personne le meilleur barbier de Bagdad, un médecin expérimenté, un chimiste très profond, un astrologue qui ne se trompe point, un grammairien achevé, un parfait rhétoricien, un logicien subtil, un mathématicien accompli dans… …   Encyclopédie Universelle

  • Lutte contre les OGM — Mouvement anti OGM Le mouvement anti OGM désigne l ensemble des actions légales, comme les campagnes de sensibilisation, ou illégales, telles que des destructions de plantations, menées par le groupe de pression qui s oppose au développement des… …   Wikipédia en Français

  • Lutte contre les organismes génétiquement modifiés — Mouvement anti OGM Le mouvement anti OGM désigne l ensemble des actions légales, comme les campagnes de sensibilisation, ou illégales, telles que des destructions de plantations, menées par le groupe de pression qui s oppose au développement des… …   Wikipédia en Français

  • Heures les plus sombres de notre histoire — Troisième Reich Großdeutsches Reich (de) (Grand Reich allemand) ↓ 1933   1945 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”