- Équation de Michaelis Menten
-
Équation de Michaelis-Menten
L’équation de Michaelis-Menten permet de décrire la cinétique d'une réaction catalysée par une enzyme agissant un substrat unique pour donner un produit. Elle relie la vitesse de la réaction à la concentration de substrat et à des paramètres constants, caractéristiques de l'enzyme. L'équation de Michaelis-Menten est un formalisme simplifié, adapté à de nombreuses enzymes. Elle ne permet cependant pas de rendre compte de comportements complexes, comme la multiplicité des substrats ou l'existence de plusieurs sites actifs présentant des comportements coopératifs ou anticoopératifs (allostérie)
Cette équation fut proposée en 1913 par l'allemand Leonor Michaelis et la canadienne Maud Menten. Selon leur modèle, l'équation décrivant la vitesse de réaction enzymatique est la suivante :
![v_{i} = {v_{max} \cdot [S] \over K_{M} + [S]}](/pictures/frwiki/48/0f7666b7297bcbbfd5e35d7f07e07ec5.png)
Avec :
- vi : vitesse initiale (c’est-à-dire en absence de produit) de la réaction enzymatique pour une concentration de substrat [S] (en µmol/min)[1] ;
- vmax : vitesse initiale maximale mesurée pour une concentration saturante de substrat (en µmol/min)[1] ;
- [S] : Concentration en substrat (en mol/L)[1] ;
- KM : Constante de Michaelis spécifique de l'enzyme. C'est la concentration en substrat pour laquelle la vitesse initiale de la réaction est égale à à la moitié de la vitesse initiale maximale
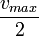 (en mol/L)[1]. Elle correspond à l'inverse de la constante d'affinité apparente du substrat pour l'enzyme.
(en mol/L)[1]. Elle correspond à l'inverse de la constante d'affinité apparente du substrat pour l'enzyme.
Graphiquement, l'équation de Michaelis-Menten est une branche d'hyperbole.
En pratique, on détermine les constantes de l'enzyme KM et vmax par la représentation des inverses (représentation de Lineweaver et Burk) qui est une droite d'équation![{1 \over v_{i}} = ({K_{M} \over v_{max}} \times {1 \over [S]}) + {1 \over v_{max}}](/pictures/frwiki/50/26f8dc075e0d996b35d02eb1c722648d.png)
Pour un graphique de vi en fonction de [S] alors, la pente est
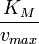 et l'ordonnée à l'origine est
et l'ordonnée à l'origine est 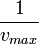 , d'où
, d'où 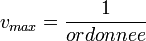 et
et 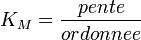 .
.Démonstration
Démonstration de l'équation de Michaelis-Menten
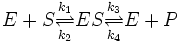
Avec k1,k2,k3,k4 les constantes de vitesse des réactions.
L'analyse de Michaelis-Menten se fait sous deux hypothèses simplificatrices :
- Pas de réaction inverse. On se place dans des conditions initiales où il n'y a pas de produit P dans le test enzymatique. On analyse la vitesse initiale de la réaction, avant que le produit ait le temps de s'accumuler. La catalyse est alors très déplacée dans le sens de la synthèse des produits, la réaction inverse dont la vitesse est k4[E][P] est alors pratiquement inexistante, puisque [P]≈0.
- Hypothèse dite du pré-équilibre rapide. On suppose que le premier équilibre dans l'équation ci-dessus, dépendant des constantes cinétiques k1 et k2 est très rapide devant l'étape de catalyse proprement dite, déterminée par k3, qui est en générale limitante. Ceci revient à dire qu'à tout instant on a
![\frac{d[ES]}{dt}=0](/pictures/frwiki/55/7fbca927118ba53cac700d6b4d8f65be.png)
Le système se simplifie alors de la manière suivante :
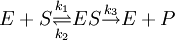
![v = k_3 \times [ES]](/pictures/frwiki/97/a2e5463ab0c1c01af964a2737e3039bd.png)
La vitesse de formation du complexe [ES] est
![v = k_1 \times [E] \times [S]](/pictures/frwiki/97/a1cb329dce4f87df6efb68d53d179c4a.png)
La vitesse d'élimination du complexe [ES] est![v = (k_2+k_3) \times [ES]](/pictures/frwiki/52/41954c9539102e3c7c3a93469cc93fd3.png)
Pendant la phase stationnaire, la concentration du complexe enzyme-substrat [ES] est constante. Donc la vitesse de formation de ce complexe [ES] doit être égale à celle de dissociation.
![k_1 \times [E] \times [S] = (k_2+k_3) \times [ES]](/pictures/frwiki/51/3666db2238fef52fb3092fa868ac22e3.png)
Soit
![[ES] = \frac{k_1 \times [E] \times [S]}{(k_2+k_3)}](/pictures/frwiki/53/5f7eb9489dc829d6cfb317c1470b10bf.png)
- On trouve une constante nommée constante de Michaelis :
![K_m = \frac{[E] \times [S]}{[ES]} = \frac{k_3 + k_2}{k_1}](/pictures/frwiki/49/1bbc5d4edf7a6c6bca3a51d16a1e6abc.png)
Comme [ES] est difficile à déterminer expérimentalement, on cherche à s'en affranchir à l'aide d'une autre équation. La concentration en enzyme libre [E] est donné par la relation de la conservation de la quantité d'enzyme [E] = [ET] − [ES] avec [ET] la concentration totale en enzyme.
![[ES] = \frac{{([E_T] - [ES])}\times{[S]}}{K_m}](/pictures/frwiki/56/825df60836f0986bac35897eb942ca46.png)
Soit
![[ES] + \frac{{[ES]}\times{[S]}}{K_M} = \frac{{[E_T]}\times{[S]}}{K_M}](/pictures/frwiki/51/3b43b4f2d1110500755731452122fbdf.png)
En mettant [ES] en facteur dans le premier terme :
![[ES] \times \left(1 + \frac{[S]}{K_M}\right) = \frac{{[E_T]}\times{[S]}}{K_M}](/pictures/frwiki/56/8cf9b1049cea09663761d37253f2014e.png)
En mettant au même dénominateur le premier terme :
![\frac{{[ES]}\times{(K_M + [S])}}{K_M} = \frac{{[E_T]}\times{[S]}}{K_M}](/pictures/frwiki/52/44b2e5c94ebb61e76f6fb1186c6db690.png)
Soit
![[ES] =\frac{{[E_T]}\times{[S]}}{K_M} \times \frac{K_M}{K_M + [S]}](/pictures/frwiki/100/d9a1d0f7b2c1f1453e814d0f7291e2a6.png)
D'où
![[ES] =\frac{{[E_T]}\times{[S]}}{K_M + [S]}](/pictures/frwiki/100/dd2621cd6384c245b97b9e28ed771cae.png)
![v = k_3 \times [ES] = k_3 \times \frac{{[E_T]}\times{[S]}}{K_M + [S]}](/pictures/frwiki/51/36908d5dad46688f92ab21fcc5993601.png)
- À vmax : [ES] = [ET]
![v_{max} = k_3 \times [E_T]](/pictures/frwiki/55/76291319669b70efa73e8114efd8004c.png)
D'où
![\frac{v}{v_{max}} = k_3 \times \frac{{[E_T]}\times{[S]}}{K_M + [S]} \times \frac{1}{k_3 \times [E_T]}](/pictures/frwiki/55/7a5a65080f8dc4373d5488e37078c730.png)
![\frac{v}{v_{max}} = \frac{[S]}{K_M + [S]}](/pictures/frwiki/53/5f86b81ac1c28397e841b113bae5224f.png)
-
- On trouve l'équation de Michaelis :
![v = v_{max} \times \frac{v}{v_{max}} = v_{max} \times \frac{[S]}{K_M + [S]}](/pictures/frwiki/99/cfa1b5102cc31be5f23018d57e117a5e.png)
Cette équation est une expression de la vitesse initiale en fonction de deux constantes : la vitesse maximum, de la constante de Michaelis et de la concentration du substrat.
Notes
Voir aussi
Catégories : Enzymologie | Catalyse
Wikimedia Foundation. 2010.
