Équation de London

Équation de London

Effet Meissner

L'effet Meissner résulte de l'expulsion des champs magnétiques par un matériau supraconducteur.

L'effet Meissner est l'exclusion totale de tout flux magnétique de l'intérieur d'un supraconducteur. Il a été découvert par Walther Meissner et Robert Ochsenfeld en 1933 et est souvent appelé diamagnétisme parfait ou l'effet Meissner-Ochsenfeld.

L'effet Meissner est l'une des propriétés définissant la supraconductivité et sa découverte a permis d'établir que l'apparition de la supraconductivité est une transition de phase.

L'exclusion du flux magnétique est due à des courants électriques d'écrantage qui circulent à la surface du supraconducteur et qui génèrent un champ magnétique qui annule exactement le champ appliqué. Ces courants d'écrantage apparaissent quand un matériau supraconducteur est soumis à un champ magnétique.

En effet, si l'on refroidit un matériau supraconducteur en présence d'un champ magnétique, le champ est expulsé au moment de la transition supraconductrice. Tandis qu'un matériau hypothétique présentant seulement la propriété de résistance nulle maintiendrait l'intensité (et le sens) du champ magnétique, qu'il aurait possédé lors de la transition, constante en son sein ; tant que cette propriété se maintiendrait. L'effet Meissner est donc une propriété des supraconducteurs qui est distincte de la conductivité infinie. En fait, l'effet Meissner ou diamagnétisme parfait est la propriété caractéristique principale d'un supraconducteur. Mais, cela ne peut se comprendre seulement par le fait que la résistance électrique d'un supraconducteur est nulle : les courants de Foucault induits par les mouvements ultérieurs du matériau dans le champ magnétique, ne sont pas atténués.

F. London a pu décrire l'effet Meissner en postulant que dans un supraconducteur il existe un courant proportionnel au potentiel vecteur électromagnétique \vec{A}:

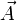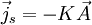
\vec{j}_s=-K \vec{A}

Cette équation n'est pas invariante de jauge, il faut donc préciser qu'on considère la jauge de Coulomb. En utilisant l'équation de Maxwell-Ampère, on obtient :

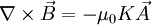
\nabla \times \vec{B} = -\mu_0 K \vec{A}

Comme \vec{B}=\nabla \times \vec{A} , en utilisant les relations du calcul vectoriel sur le double rotationnel, on trouve :

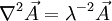
\nabla^2 \vec{A} = \lambda^{-2} \vec{A}

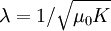où \lambda=1/\sqrt{\mu_0 K} est une longueur caractéristique. La solution de cette équation est :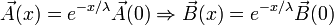

\vec{A}(x) = e^{-x/\lambda} \vec{A}(0)\Rightarrow \vec{B}(x)=e^{-x/\lambda} \vec{B}(0)

dans le cas d'un milieu supraconducteur s'étendant dans le demi-espace x > 0. La longueur λ est la longueur de pénétration du champ magnétique. Cette équation montre que les champs magnétiques ne pénètrent que la surface des supraconducteurs.

Une autre conséquence de l'effet Meissner est puisque les courants électriques (du supraconducteur) génèrent des champs magnétiques tels qu'ils annulent le champ externe, ses courants électriques s'écoulent essentiellement dans sa surface immédiate.

L'équation de London peut se déduire de la théorie de Ginzburg-Landau.

Références

  • Lev Landau et Evguéni Lifchitz, Physique théorique, tome 8 : Électrodynamique des milieux continus, éd. MIR, Moscou [détail des éditions]
  • Charles Kittel (trad. Nathalie Bardou, Évelyne Kolb), Physique de l’état solide [« Solid state physics »], 1998 [détail des éditions] 

Liens externes

Commons-logo.svg
  • Portail de la physique Portail de la physique
Ce document provient de « Effet Meissner ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équation de London de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • London equations — The London equations, developed by brothers Fritz and Heinz London in 1935, [cite journal last= London first= F. coauthors= H. London month= March title= The Electromagnetic Equations of the Supraconductor journal= Proc. Roy. Soc. (London) volume …   Wikipedia

  • Equation of time — The equation of time is the difference over the course of a year between time as read from a sundial and time as read from a clock, measured in an ideal situation (ie. in a location at the centre of a time zone, and which does not use daylight… …   Wikipedia

  • Équation aux dimensions — Analyse dimensionnelle L analyse dimensionnelle est un outil théorique servant à interpréter les problèmes à partir des dimensions des grandeurs physiques mises en jeu. Cet outil est utilisé particulièrement en physique, en chimie et en… …   Wikipédia en Français

  • Équation de Kepler — En astronomie, l équation de Kepler est une formule liant l excentricité e et l anomalie excentrique E à l anomalie moyenne M. L importance de cette équation est qu elle permet de passer des paramètres dynamiques du mouvement d un astre (l… …   Wikipédia en Français

  • Équation de Friedman — Équations de Friedmann Le contenu de cet article du Portail:Cosmologie a fait l objet d une validation par un chercheur spécialiste du domaine le 18 juillet 2007 (comparer avec la version actuelle). Il est donc en principe exempt d erreur grave.… …   Wikipédia en Français

  • Équation de Picard-Fuchs — En mathématiques, on appelle équation de Picard Fuchs une équation différentielle assez particulière, car ses solutions décrivent la variation des périodes d une courbe elliptique en termes de son paramètre modulaire (en). Définition Pour… …   Wikipédia en Français

  • Équation de Davies — L équation de Davies est une extension empirique de l Équation de Debye–Hückel qui peut être utilisée pour calculer le coefficient d activités d une solution électrolyte de concentration relativement élevée. L équation, publiée en 1938[1], a été… …   Wikipédia en Français

  • London dispersion force — Interaction energy of argon dimer. The long range part is due to London dispersion forces London dispersion forces (LDF, also known as dispersion forces, London forces, instantaneous dipole–induced dipole forces) is a type of force acting between …   Wikipedia

  • London penetration depth — In superconductivity, London penetration depth (usually denoted as lambda, or lambda L,) characterizes the typical distance to which a weak magnetic field penetrates into a superconductor.Typical values of lambda L, are between 50 and 500 nm.… …   Wikipedia

  • Camassa–Holm equation — In fluid dynamics, the Camassa–Holm equation is the integrable, dimensionless and non linear partial differential equation:u t + 2kappa u x u {xxt} + 3 u u x = 2 u x u {xx} + u u {xxx}. ,The equation was introduced by Camassa and HolmCamassa Holm …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”