- Verre de spin
-
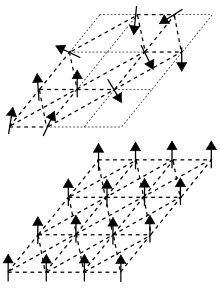Représentation schématique d'une structure aléatoire d'un verre de spins (haut) et d'un état ferromagnétique (bas).
Les verres de spin sont des alliages métalliques comportant un petit nombre d'impuretés magnétiques disposées au hasard dans l'alliage. À chaque impureté est associée un spin. Le couplage entre ces différents spins peut être plus ou moins intense - attractif ou répulsif - en fonction de la distance qui les sépare. Les physiciens les modélisent statistiquement par des spins d'Ising (plus ou moins un) couplés par des constantes aléatoires représentant le désordre. Ces constantes évoluent lentement à mesure que le verre de spin vieillit et que les impuretés diffusent, c'est pourquoi ces couplages sont dits gelés, ou indépendant du temps (quenched). Souvent, on considère que ces couplages suivent une distribution gaussienne.
En physique statistique, parler des verres de spin revient à parler de ces modèles (cf ci-dessous). Ces verres de spin constituent le paradigme des systèmes désordonnés, qui, avec la physique des processus hors équilibre, constituent une grande part des travaux de ce domaine dans les dernieres années. Les verres de spin sont dits frustrés : selon des chemins différents, deux spins se donnent des instructions contradictoires. Les modèles les plus connus sont ceux d'Edward Anderson où l'on ne considère que les couplages entre plus proches voisins sur réseau hypercubique, et de Sherington et Kirpatrick[1], où toutes les paires de spins interagissent entre elles (graphe complet), et qui est censé tenir compte des interactions à grande distance. Ces modèles se résument donc à se donner un hamiltonien, ainsi qu'une distribution des couplages.
Pourquoi les verres de spin sont-ils appelés verres ? Un verre est un état de la matière à mi-chemin entre le liquide et le solide et qui possède un grand nombre d'états métastables de basse énergie. Quand le verre refroidit, il est généralement bloqué, non pas dans l'état fondamental, mais dans un de ces états métastables de basse énergie. Il en va de même des verres de spins qui possèdent un paysage composé de beaucoup d'états métastables dans les basses énergies. Il met un très grand temps pour franchir les différentes barrières et rejoindre finalement l'état fondamental (vieillissement). C'est pourquoi les constantes de couplages sont considérées comme gelées relativement aux configurations de spin (variables dynamiques), et qu'il y a lieu de considérer deux échelles de temps.
Les états purs de basse énergie présentent des propriétés d'ultramétricité. Leur répartition est ultramétrique.
Les difficultés rencontrées pour calculer l'énergie libre des verres de spin a donné naissance à la méthode des répliques.
Les applications des verres de spin sont nombreuses : depuis les problèmes d'optimisation (économie, etc.) jusqu'en biologie (modélisation des neurones, apprentissages).
Notes et rérérences
- (en) David Sherrington et Scott Kirkpatrick, « Solvable model of a spin-glass », dans Physics Review Letters, vol. 35, no 26, 1975, p. 1792-1796 [lien DOI]
Ouvrages
- Un ouvrage de référence dans ce domaine est spin glass theory and beyond de Parisi, Mézard etc.
- Viktor Dotsenko, An Introduction to the theory of spin glasses and neural networks, World Scientific, 1994
Liens externes
- (fr) [ps] Verres de spin et optimisation combinatoire : notes de séminaire de M. Talagrand présentant quelques résultats et enjeux sur les verres de spin, 1999.
Wikimedia Foundation. 2010.
