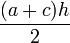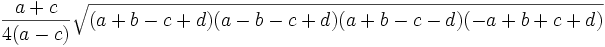Trapèze rectangle

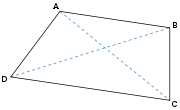
Un trapèze est un quadrilatère, possédant au moins deux côtés opposés parallèles. Ces deux côtés parallèles sont appelés bases.

Avec cette définition, les quadrilatères ABCD et ABDC de la figure sont tous deux des trapèzes (dont les côtés (AB) et (CD) sont parallèles).

Certains auteurs imposent comme condition supplémentaire la convexité du quadrilatère, ce qui conduit à exclure les « trapèzes croisés » tels que ABDC.

Sommaire 1 Propriétés 2 Cas particuliers 3 Aire du trapèze 4 Théorème du trapèze 5 Méthode des trapèzes

Propriétés

Un quadrilatère convexe est un trapèze si et seulement s’il possède une paire d’angles consécutifs de somme égale à 180 degrés ou π radians. La somme des deux autres angles est alors la même. Par exemple : Ici les deux paires d'angles ont pour sommets (A,D) et (B,C).

Attention : Dans un trapèze la somme de deux angles consécutifs n'est pas toujours égale à 180 degrés. (exemple : les angles de sommets A et B)

Cas particuliers

• Un trapèze est qualifié de trapèze rectangle dès qu’il possède un angle droit.

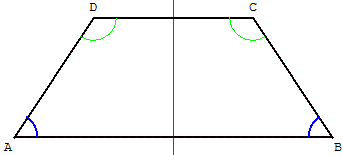
Un trapèze est qualifié d’isocèle lorsqu'il vérifie l'une des propriétés équivalentes suivantes :

• Deux angles adjacents à une même base sont égaux.
• Les côtés non parallèles sont de même longueur.
• Les deux bases du trapèze ont la même médiatrice, et celle-ci est un axe de symétrie du trapèze.

Un trapèze convexe dont les bases ont même longueur est un parallélogramme

Aire du trapèze

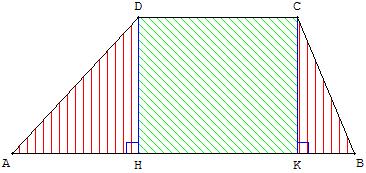
L’aire du trapèze convexe vaut le produit de sa hauteur par la demi-somme de ses bases.

C’est-à-dire, soit h la hauteur, a la première base, et c la deuxième.

Ceci peut se démontrer facilement en remarquant que le trapèze est un rectangle auquel on accole deux triangles.

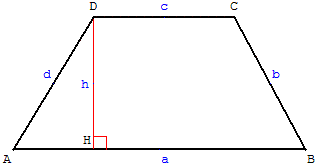
Une autre formule donne l'aire du trapèze lorsque ne sont connues que les quatre longueurs a, b, c, d des quatre côtés :

Attention, pour cette formule a et c représentent les deux bases parallèles du trapèze et a la plus longue des deux.

Théorème du trapèze

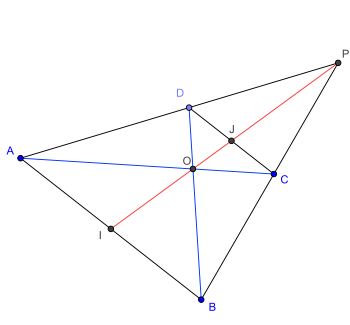
Dans un trapèze, la droite joignant le point d'intersection des côtés non parallèles au point d'intersection des diagonales, passe par les milieux des côtés parallèles.

En effet, soit ABCD est un trapèze de bases [AB] et [CD] ayant pour milieux I et J. Les diagonales [AC] et [BD] se coupent en O. Les droites (BC) et (AD) se coupent en P.

Les points I, J, O et P sont alignés.

Démonstration avec l'homothétie :

Utiliser les propriétés des homothéties transformant le segment [AB] en [CD].

Réciproque : CDP est un triangle, J le milieu de [CD], O un point de la droite (PJ) distinct de P, de J et du symétrique de J par rapport à P.
(CO) coupe (PD) en A et (DO) coupe (PC) en B.

Les droites (AB) et (CD) sont parallèles et le point I, intersection de (AB) et (PJ), est le milieu de [AB].

Méthode des trapèzes

Article principal : Méthode des trapèzes

La méthode d’intégration approchée, dite des trapèzes, décrite par Isaac Newton et son élève Roger Cotes, consiste à remplacer les arcs de courbe successifs M_iM_i+1 par les segments [M_iM_i+1] : c'est une interpolation linéaire.

La méthode des trapèzes est plus précise que la méthode élémentaire, dite des rectangles, correspondant aux sommes de Riemann, consistant à remplacer la fonction donnée par une fonction en escalier.

• Portail de la géométrie