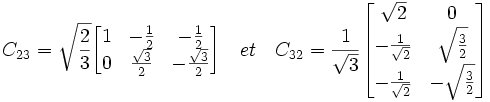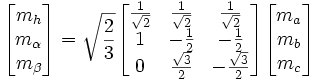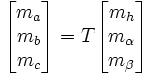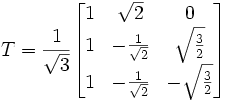Transformée de concordia
- Transformée de concordia
-
Transformée de Concordia
La transformée de Concordia, est un outil mathématique utilisé en électrotechnique afin de modéliser un système triphasé grâce à un modéle diphasé.
Philosophie de la transformée de Concordia
Exemple
Un système diphasé constitué de deux bobines perpendiculaires l'une par rapport à l'autre et parcourues par des courants déphasés entre eux de π / 2 permet de créer un champ tournant à la vitesse ω.
Schéma
Un système triphasé constitué de bobines et de courants déphasés entre eux de 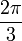 permet de créer un champ tournant à la vitesse ω.
permet de créer un champ tournant à la vitesse ω.
Schéma
Mise en équations
On peut modéliser le champ tournant créé par système triphasé par un système diphasé grâce aux transformations suivantes :
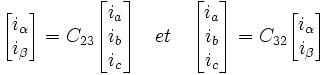
avec :
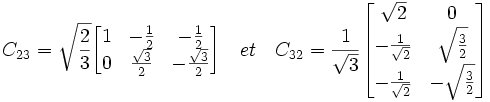
Si on veut conserver la composante homopolaire les transformations deviennent :
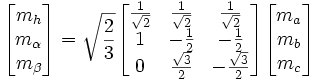
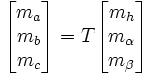
où T est la matrice de Concordia. Il existe aussi une transformation de Clarke qui est la même que celle de Concordia mais qui n'est pas normée. Elle ne conserve donc pas la puissance lors des opérations matricielles.
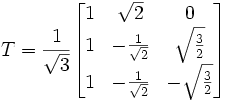
Voir aussi
 Portail de l’électricité et de l’électronique
Portail de l’électricité et de l’électronique
Catégories : Électrotechnique | Matrice
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Transformée de concordia de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Transformee de Concordia — Transformée de Concordia La transformée de Concordia, est un outil mathématique utilisé en électrotechnique afin de modéliser un système triphasé grâce à un modéle diphasé. Sommaire 1 Philosophie de la transformée de Concordia 1.1 Exemple 2 Mise… … Wikipédia en Français
Transformée de Concordia — La transformée de Concordia, est un outil mathématique utilisé en électrotechnique afin de modéliser un système triphasé grâce à un modéle diphasé. Sommaire 1 Philosophie de la transformée de Concordia 1.1 Exemple 2 Mise en équations … Wikipédia en Français
Concórdia — Concordia Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Concordia est un mot latin qui signifie « harmonie, concorde » (littéralement tous les cœurs ensemble) ; il est utilisé dans ce… … Wikipédia en Français
Transformee de Park — Transformée de Park La transformée de Park, est un outil mathématique utilisé en électrotechnique afin de réaliser un changement de repère dans un système d axe diphasé ou triphasé. Elle est généralement utilisée pour passer d un repère… … Wikipédia en Français
Transformée de park — La transformée de Park, est un outil mathématique utilisé en électrotechnique afin de réaliser un changement de repère dans un système d axe diphasé ou triphasé. Elle est généralement utilisée pour passer d un repère « fixe » lié au… … Wikipédia en Français
Concordia — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Concordia est un mot latin qui signifie « harmonie, concorde » (littéralement tous les cœurs ensemble) ; il est utilisé dans ce sens dans… … Wikipédia en Français
Transformée de Park — La transformée de Park, est un outil mathématique utilisé en électrotechnique afin de réaliser un changement de repère dans un système d axe diphasé ou triphasé. Elle est généralement utilisée pour passer d un repère « fixe » lié au… … Wikipédia en Français
Transformée de Clarke — La transformée de Clarke, est un outil mathématique utilisé en électrotechnique afin de modéliser un système triphasé grâce à un modéle diphasé Un système triphasé constitué de bobines et de courants déphasés entre eux de permet de créer un champ … Wikipédia en Français
Commande Vectorielle — La Commande vectorielle est un terme générique désignant l ensemble des commandes tenant compte en temps réel des équations du système qu elle commande. Le nom de ces commandes vient du fait que les relations finales sont vectorielles à la… … Wikipédia en Français
Commande vectorielle — La commande vectorielle est un terme générique désignant l ensemble des commandes tenant compte en temps réel des équations du système qu elle commande. Le nom de ces commandes vient du fait que les relations finales sont vectorielles à la… … Wikipédia en Français
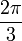 permet de créer un champ tournant à la vitesse ω.
permet de créer un champ tournant à la vitesse ω.