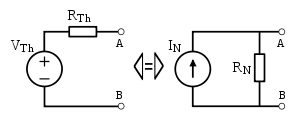
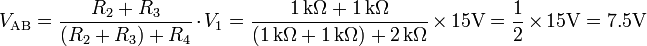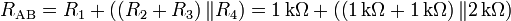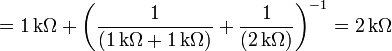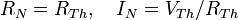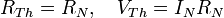- Transformation Norton-Thévenin
-
Théorème de Thévenin
Le théorème de Thévenin a été initialement découvert par le scientifique allemand Hermann von Helmholtz en 1853, puis en 1883 par l'ingénieur télégraphe français Léon Charles Thévenin. Ce théorème est une propriété électronique qui se déduit principalement des propriétés de linéarité[1] et du principe de superposition qui en découle. Il s'utilise pour convertir une partie d'un réseau complexe en un dipôle plus simple.
Sommaire
Énoncé
Un réseau électrique linéaire vu de deux points est équivalent à un générateur de tension parfait dont la force électromotrice est égale à la différence de potentiels à vide entre ces deux points, en série avec une résistance égale à celle que l'on mesure entre les deux points lorsque les générateurs indépendants sont rendus passifs.
Démonstration du théorème de ThéveninLa démonstration de ce théorème repose sur le principe de superposition, ce qui permet d'étendre la généralité de son application à tous dispositifs électroniques qui fonctionnent linéairement.
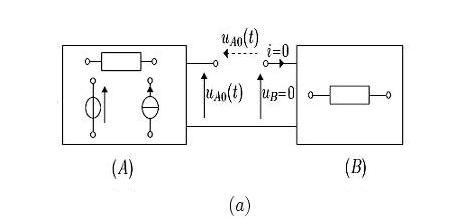
On peut imaginer la situation où l'on relie deux dipôles linéaires désignés respectivement par les lettres A et B, le but de la démarche est alors de trouver un schéma équivalent au dipôle A de sorte que son comportement vis à vis du dipôle B reste identique.
Avant de relier les dipôles A et B, les tensions à vide entre leurs bornes sont respectivement
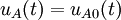 et
et 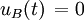 , car on considère tout d'abord pour simplifier la démonstration que le dipôle B ne contient pas de sources électriques et que toutes les grandeurs électriques, en circuit ouvert, y sont initialement nulles (figure a).
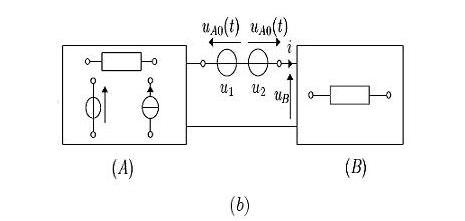
, car on considère tout d'abord pour simplifier la démonstration que le dipôle B ne contient pas de sources électriques et que toutes les grandeurs électriques, en circuit ouvert, y sont initialement nulles (figure a).On peut ensuite relier les deux dipôles à l'aide d'un court-cicuit qu'on remplace, toutefois de manière équivalente, par deux sources de tension en série
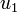 et
et 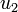 qui ont une même amplitude égale à
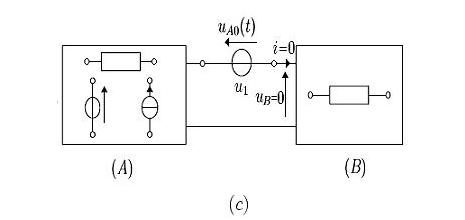
qui ont une même amplitude égale à 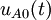 mais des orientations opposées (figure b). Dans ce nouveau montage, les courants et tensions se voient alors, par application du principe de superposition, comme le résultat de l'action cumulée de deux influences: celle de
mais des orientations opposées (figure b). Dans ce nouveau montage, les courants et tensions se voient alors, par application du principe de superposition, comme le résultat de l'action cumulée de deux influences: celle de 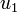 et des sources électriques situées dans A d'une part (figure c) et celle de
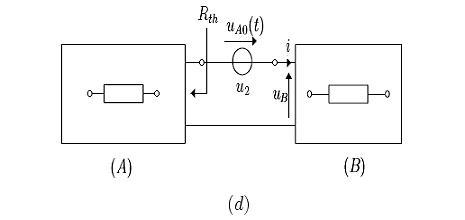
et des sources électriques situées dans A d'une part (figure c) et celle de 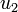 d'autre part (figure d). Cependant, il apparait clairement que la première de ces influences est équivalente à la situation où les deux dipôles se trouvaient en circuit ouvert et qu'elle ne modifie donc pas les grandeurs électriques de B. La source de tension
d'autre part (figure d). Cependant, il apparait clairement que la première de ces influences est équivalente à la situation où les deux dipôles se trouvaient en circuit ouvert et qu'elle ne modifie donc pas les grandeurs électriques de B. La source de tension 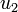 d'amplitude
d'amplitude 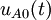 mis en série avec le dipôle A dans lequel a été annulé l'influence de toutes sources électriques indépendantes peut ainsi sembler comme à l'origine des courants et tensions du dipôle B.
mis en série avec le dipôle A dans lequel a été annulé l'influence de toutes sources électriques indépendantes peut ainsi sembler comme à l'origine des courants et tensions du dipôle B.Lorsque le dipôle B contient également des sources électriques indépendantes, on peut encore à l'aide du principe de superposition revenir à la situation précédente et utiliser le même raisonnement. Il suffit pour retrouver cette situation d'annuler les sources électriques, tour à tour dans chaque dipôle, cela permettant de déterminer successivement les dipôles de Thévenin équivalents à A et à B.
Détermination du modèle de Thévenin
Soit un circuit composé de plusieurs sources et de plusieurs résistances possédant deux bornes A et B entre lesquelles est raccordée une charge :
- La tension de Thévenin
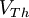 est la tension calculée ou mesurée, entre les bornes A et B lorsque la charge est déconnectée (tension à vide).
est la tension calculée ou mesurée, entre les bornes A et B lorsque la charge est déconnectée (tension à vide). - La résistance de Thévenin
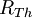 est la résistance calculée, ou mesurée, entre les bornes A et B lorsque la charge est déconnectée et que les sources sont éteintes : les sources de tension indépendantes sont remplacées par un court-circuit et les sources de courant indépendantes par un circuit ouvert.
est la résistance calculée, ou mesurée, entre les bornes A et B lorsque la charge est déconnectée et que les sources sont éteintes : les sources de tension indépendantes sont remplacées par un court-circuit et les sources de courant indépendantes par un circuit ouvert.
Lorsque la tension de Thévenin est connue, il existe trois autres méthodes pratiques pour mesurer la résistance de Thévenin.
- La première consiste à remplacer la charge par une résistance dont la valeur est connue et à prendre la tension aux bornes de cette résistance.
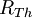 se résout facilement car elle devient alors la seule inconnue de l'équation découlant du théorème du diviseur de tension.
se résout facilement car elle devient alors la seule inconnue de l'équation découlant du théorème du diviseur de tension. - La deuxième méthode, proche de la première, est celle dite de la demi-tension : on utilise une résistance variable au lieu d'une résistance fixe et on fait varier la valeur de la résistance jusqu'à avoir
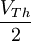 , les deux résistances sont alors égales.
, les deux résistances sont alors égales. - La dernière méthode fait appel au courant de Norton. Si celui-ci est connu, on utilise la formule suivante:
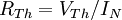 où
où 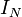 est le courant calculé ou mesuré, entre les bornes A et B lorsqu'elles sont court-circuitées.
est le courant calculé ou mesuré, entre les bornes A et B lorsqu'elles sont court-circuitées.
Le théorème de Thévenin s'applique aussi aux réseaux alimentés par des sources alternatives. L'ensemble des résultats est applicable en considérant la notion d'impédance en lieu et place de celle de résistance.
Exemple
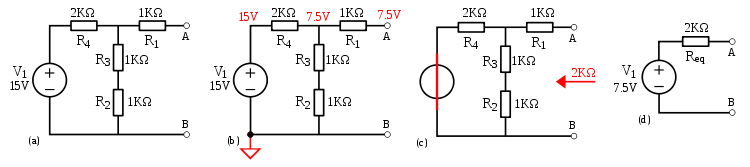
- En (a): Circuit originel.
- En (b): Calcul de la tension aux bornes de AB.
(Notez que R1 n'est pas prise en considération, car les calculs ci-dessus sont faits en circuit ouvert entre A et B, par suite, il n'y a pas de courant qui passe à travers R1 et donc aucune chute de tension n'y apparait)
- En (c): Calcul de la résistance équivalente aux bornes AB en court-circuitant V1.
- En (d): Circuit équivalent de Thévenin. Celui-ci nous permet de trouver aisément le courant dans un dipôle quelconque relié entre les bornes A et B sans qu'on ait à résoudre le circuit au complet.
Conversion entre un circuit de Thévenin et de Norton
On passe directement d'un circuit de Thévenin à un circuit de Norton et inversement, à l'aide des formules suivantes:
- De Thévenin à Norton;
- De Norton à Thévenin;
Notes et références
- ↑ José-Philippe Pérez, « La main à la pâte, oui mais avec la Tête ! », Bulletin de l'union des physiciens, n°906, juillet/août/septembre 2008, page 988.
- Léon C. Thévenin, « Extension de la loi d’Ohm aux circuits électromoteurs complexes », dans Annales Télégraphiques, tome 10, 1883, p. 222-224
- Léon C. Thévenin, « Sur un nouveau théorème d’électricité dynamique », dans Compte rendu des Séances de l’Académie des Sciences, 1883, p. 159-161
Voir aussi
Articles connexes
- Théorème de Norton
- Électricité
- Lois de Kirchhoff (loi des mailles et loi des nœuds)
- Loi d'Ohm
- Principe de superposition
- Théorème de Millman
- Théorème de réciprocité
- Théorème de Tellegen
- Circuit ouvert
Liens externes
- [pdf](en) Introduction du théorème de Thévenin.
- [pdf](en) Historique du concept de circuit équivalent.
- (en) Autres preuves du théorème:[1], [2], [3],[4].
- Portail de la physique
- Portail de l’électricité et de l’électronique
Catégories : Théorie électrique | Théorème de physique - La tension de Thévenin
Wikimedia Foundation. 2010.