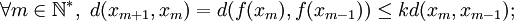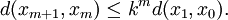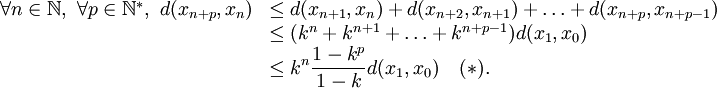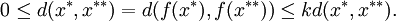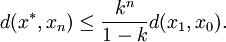Théorème du point fixe de Picard

Application contractante

En mathématiques, une application contractante est une application $k$ -lipschitzienne avec 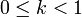$0\leq k <1$ . Les applications contractantes sont la matière de base du théorème de point fixe le plus simple et le plus utilisé.

Sommaire

1 Théorème du point fixe pour une application contractante
- 1.1 Existence
- 1.2 Unicité
2 Approximations successives
3 Applications classiques

Théorème du point fixe pour une application contractante

Théorème du point fixe pour une application contractante — Soit $E$ un espace métrique complet (non vide) et $f$ une application contractante de $E$ dans $E$ . Il existe un point fixe unique $x *$ de $f$ dans $E$ , c'est-à-dire tel que $f (x *) = x *$ . De plus toute suite d'éléments de E vérifiant la récurrence $x n + 1 = f (x n)$ converge vers $x *$ .

Démonstration

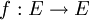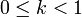Soit $(E, d)$ un espace métrique non vide et soit $f:E \rightarrow E$ une application contractante de rapport $k$ , avec $0\leq k <1$ .

Existence

Soit 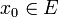$x_0\in E$ et soit 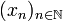$(x_n)_{n \in \mathbb N}$ la suite définie par son premier terme ( $x 0$ ) et la récurrence $x n + 1 = f (x n)$ pour tout 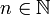$n \in \mathbb{N}$ . Il s'agit d'une suite de Cauchy de $E$ . En effet,

$\forall m \in \mathbb N^*,\ d(x_{m+1},x_m)=d(f(x_m),f(x_{m-1}))\le k d(x_m,x_{m-1});$

et par récurrence

$d(x_{m+1},x_m) \le k^m d(x_1,x_0).$

On en déduit par application réitérée de l'inégalité triangulaire :

$\begin{array}{ll} \forall n \in \mathbb N,\ \forall p \in \mathbb N^*,\ d(x_{n+p},x_n) & \le d(x_{n+1},x_n)+d(x_{n+2},x_{n+1})+\ldots+d(x_{n+p},x_{n+p-1})\\ & \le (k^n+k^{n+1}+\ldots+k^{n+p-1}) d(x_1,x_0)\\& \le \displaystyle k^n\frac {1-k^p}{1-k} d(x_1,x_0) \quad (*).\end{array}$

Ce dernier membre tend vers zéro quand $n$ tend vers l'infini, donc on a bien une suite de Cauchy.

Comme $E$ est complet, cette suite de Cauchy converge vers une limite $x *$ . De plus de $x n + 1 = f (x n)$ , on déduit en passant à la limite et en utilisant la continuité de $f$ (car c'est une application lipschitzienne) que $f (x *) = x *$ , ce qui montre l'existence.

Unicité

Soit $x *$ et $x * *$ deux points fixes de f. On a alors

$0\leq d(x^*,x^{**}) = d(f(x^*),f(x^{**}))\leq k d(x^*,x^{**}).$

Et puisque 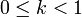$0\leq k <1$ , on a alors 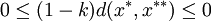$0\leq (1-k)d(x^*,x^{**}) \leq 0$ , d'où $d (x *, x * *) = 0$ , puis $x * = x * *$ , ce qui montre l'unicité.

Approximations successives

Ce résultat donne un algorithme de calcul du point fixe (c'est la méthode des approximations successives) contrairement à d'autres théorèmes de point fixe qui nous assurent seulement de l'existence de points fixes sans indiquer comment les déterminer. De plus en passant à la limite pour $p$ dans l'inégalité (*) et en utilisant la continuité de la distance $d$ , on obtient (sans connaître exactement $x *$ ) un majorant (souvent "pessimiste") de l'erreur:

$d(x^*,x_n) \leq \frac {k^n}{1-k} d(x_1,x_0).$

Applications classiques

Résolution d'équations numériques, voir notamment méthode de Newton
Résolution approchée de systèmes linéaires par itération
Résolution d'équation différentielle : théorème de Cauchy-Lipschitz
Théorème des fonctions implicites

Portail de la géométrie

Ce document provient de « Application contractante ».

Catégories : Analyse réelle | Analyse numérique | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème du point fixe de Picard de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Théorème du point fixe de Brouwer — En 1886 Henri Poincaré démontre un résultat équivalent au théorème du point fixe de Brouwer. L énoncé exact est prouvé pour la dimension trois par Piers Bohl pour la première fois en 1904, puis par Jacques Hadamard dans le cas général en 1910.… … Wikipédia en Français
Théorème du point fixe — Théorèmes de point fixe En analyse, un théorème de point fixe est un résultat qui permet d affirmer qu une fonction f admet sous certaines conditions un point fixe. Ces théorèmes se révèlent être des outils très utiles en mathématiques,… … Wikipédia en Français
Theoremes de point fixe — Théorèmes de point fixe En analyse, un théorème de point fixe est un résultat qui permet d affirmer qu une fonction f admet sous certaines conditions un point fixe. Ces théorèmes se révèlent être des outils très utiles en mathématiques,… … Wikipédia en Français
Théorèmes de point fixe — En analyse, un théorème de point fixe est un résultat qui permet d affirmer qu une fonction f admet sous certaines conditions un point fixe. Ces théorèmes se révèlent être des outils très utiles en mathématiques, principalement dans le domaine de … Wikipédia en Français
Theoreme de Stampacchia — Théorème de Stampacchia Le théorème de Stampacchia est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 Cas symétrique … Wikipédia en Français
Théorème de stampacchia — Le théorème de Stampacchia est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 Cas symétrique … Wikipédia en Français
Théorème de Stampacchia — Le théorème de Stampacchia est un théorème d analyse fonctionnelle. C est un raffinement du théorème de Lax Milgram. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 … Wikipédia en Français
Theoreme de Cauchy-Lipschitz — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Théorème de Picard-Lindelöf — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Théorème de cauchy-lipschitz — Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème du point fixe de Picard

Application contractante

Sommaire