Théorème du papillon

Théorème du papillon
Page d'aide sur l'homonymie Ne doit pas être confondu avec le lemme de Zassenhaus (en) ou « lemme du papillon » .
Figure du théorème du papillon

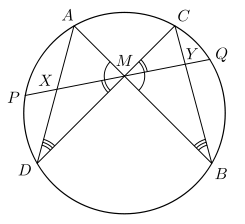
Le théorème du papillon est un théorème de la géométrie euclidienne. Son nom provient de la similitude entre la disposition des deux triangles (voir figure) et les ailes d'un papillon.

Énoncé

Théorème du papillon — Soit M le milieu d'une corde arbitraire [PQ] d'un cercle. Quatre autres cordes sont tracées : [AB] et [CD] passant par M, puis les cordes [AD] et [BC], ces deux dernières intersectant la corde [PQ] en X et Y respectivement. Alors, MX = MY.

Démonstration

Les notations sont celles de la figure et correspondent à l'énoncé ci-dessus.

On nomme X1 le pied de la hauteur issue de X dans le triangle AXM. De même on nomme X2 pied de la hauteur issue de X dans le triangle DXM, Y1 pied de la hauteur issue de Y dans le triangle BYM et Y2 pied de la hauteur issue de Y dans le triangle CYM.

On remarque alors que les triangles MXX1 et MYY1 sont semblables car \widehat{MX_{1}X}=\widehat{MY_{1}Y} (ce sont des angles droits) et \widehat{X_{1}MX}=\widehat{Y_{1}MY} car ils sont opposés par le sommet ; d'où : \frac{MX}{XX_1}=\frac{MY}{YY_1}.

De même MXX2 est semblable à MYY2 et \frac{MX}{XX_2}=\frac{MY}{YY_2}.

On procède de la même manière pour les triangles semblables AXX1 et CYY2 sachant que \widehat{XAX_{1}}=\widehat{YCY_{2}} car ces angles interceptent le même arc (voir Théorème de l'angle inscrit et de l'angle au centre) ; d'où : \frac{AX}{XX_1}=\frac{CY}{YY_2}.

De même DXX2 est semblable à BYY1 et \frac{DX}{XX_2}=\frac{BY}{YY_1}.

On a donc :

\left( \frac{MX}{MY} \right)^2 = \frac{XX_1}{YY_1} \cdot \frac{XX_2}{YY_2}

= \frac{AX.DX}{CY.BY}
= \frac{PX.QX}{PY.QY} (voir Puissance d'un point par rapport à un cercle)
= \frac{(PM-MX)(QM+MX)}{(PM+MY)(QM-MY)}
= \frac{PM^2-MX^2}{PM^2-MY^2} car PM = QM

Ainsi MX2 = MY2, ce sont des longueurs donc MX = MY.

M est bien le milieu du segment [XY].

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème du papillon de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Theoreme du papillon — Théorème du papillon Figure du théorème du papillon Le théorème du papillon est un théorème de la géométrie euclidienne. Son nom provient de la similitude entre la disposition des deux triangles (voir figure) et les ailes d un papillon. Énoncé …   Wikipédia en Français

  • Theoreme d'inversion locale — Théorème d inversion locale En mathématiques, le théorème d inversion locale est un résultat de géométrie différentielle. Il indique que si une fonction f est continûment différentiable en un point a, si cette différentielle est une bijection… …   Wikipédia en Français

  • Théorème d'inversion locale — En mathématiques, le théorème d inversion locale est un résultat de géométrie différentielle. Il indique que si une fonction f est continûment différentiable en un point, si sa différentielle en ce point est une bijection bicontinue, c est à dire …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

  • Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Chaotique — Théorie du chaos Pour les articles homonymes, voir Chaos. Attracteur étrange de Lorenz La théorie du chaos traite des sys …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”