Théorème de plongement de nash

Théorème de plongement de Nash

Le théorème de plongement de Nash (d'après le nom du mathématicien John Forbes Nash) affirme que toute variété riemannienne peut être plongée de manière isométrique dans un espace euclidien de type $\mathbb{R}^n$ .

"De manière isométrique" veut dire "conservant la longueur des courbes". Une conséquence de ce théorème est que toute variété riemannienne peut être vue comme une sous-variété d'un espace euclidien.

Il existe deux théorèmes de plongement de Nash :

Le premier (1954), portant sur les variétés de classe C¹. Il est peu intuitif mais se démontre facilement.
Le second (1956), portant sur les variétés de classe C^k où k ≥ 3. Celui-ci est plus intuitif que le premier, mais se démontre difficilement.

Sommaire

1 Théorème de plongement C¹ (Nash-Kuiper)
2 Théorème de plongement C^k
3 Bibliographie
4 Voir aussi

Théorème de plongement C¹ (Nash-Kuiper)

Soient (M, g) une variété riemannienne de dimension m et 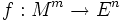$f:M^m\to E^n$ un plongement lisse et court 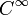$C^\infty$ dans un espace euclidien $E n$ où 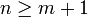$n\ge m+1$ . Alors pour tout $ε > 0$ il existe un plongement 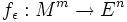$f_\epsilon:M^m\to E^n$ ayant les propriétés suivantes :

(i)

f ε

est de classe

C 1

(ii)

f ε

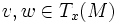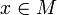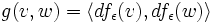est isométrique, i.e. pour tout couple de vecteurs $v,w\in T_x(M)$ dans l'espace tangent en $x\in M$ on a $g(v,w)=\langle df_\epsilon(v),df_\epsilon(w)\rangle$ .

(iii)

| f (x) - f ε (x) | < ε

pour tout $x\in M$ .

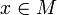En particulier, toute variété riemannienne de dimension m admet une isométrie de classe C¹ dans un espace euclidien de dimension 2 m.

Ce théorème a beaucoup de conséquences contre-intuitives. Par exemple : toute surface orientée et fermée peut être $C 1$ -plongée dans une boule de taille arbitrairement petite d'un espace euclidien à 3 dimensions (d'après la formule de Gauss, cela n'est plus vrai pour les plongements de classe $C 3$ ; la question est ouverte pour les plongements $C 2$ )

Théorème de plongement C^k

Soient (M, g) une variété riemannienne de dimension m (analytique ou de classe C^k avec k > 3). Alors il existe un nombre n ( $n = m 2 + 5 m + 3$ suffit) et un plongement injectif 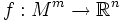$f : M^{m} \to \mathbb{R}^n$ (également analytique ou de classe C^k) tel qu'en tout point p de M,

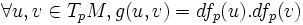$\forall u,v \in T_p M, g(u,v) = df_p(u).df_p(v)$ où . est le produit scalaire canonique de $\mathbb{R}^n$ .

Bibliographie

N.H.Kuiper: "On C¹-isometric imbeddings I", Nederl. Akad. Wetensch. Proc. Ser. A., 58 (1955), pp 545–556.
John Nash: "C¹-isometric imbeddings", Annals of Mathematics, 60 (1954), pp 383–396.
John Nash: "The imbedding problem for Riemannian manifolds", Annals of Mathematics, 63 (1956), pp 20–63.
John Nash: "Analyticity of the solutions of implicit function problem with analytic data" Annals of Mathematics, 84 (1966), pp 345–355.

Voir aussi

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de plongement de Nash ».

Catégories : Géométrie différentielle | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de plongement de nash de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Theoreme de plongement de Nash — Théorème de plongement de Nash Le théorème de plongement de Nash (d après le nom du mathématicien John Forbes Nash) affirme que toute variété riemannienne peut être plongée de manière isométrique dans un espace euclidien de type . De manière… … Wikipédia en Français
Théorème de plongement de Nash — En géométrie différentielle, le théorème de plongement de Nash, dû au mathématicien John Forbes Nash, affirme que toute variété riemannienne peut être plongée de manière isométrique dans un espace euclidien. « De manière isométrique »… … Wikipédia en Français
Théorème d'encastrement de Nash — Théorème de plongement de Nash Le théorème de plongement de Nash (d après le nom du mathématicien John Forbes Nash) affirme que toute variété riemannienne peut être plongée de manière isométrique dans un espace euclidien de type . De manière… … Wikipédia en Français
John Forbes Nash — Pour les articles homonymes, voir John Nash. John Forbes Nash Jr. John Nash en 2000 Naissance … Wikipédia en Français
John F. Nash — John Forbes Nash Pour les articles homonymes, voir John Nash. John Forbes Nash Jr en 2006 John Forbes Nash Jr (né le … Wikipédia en Français
John Forbes Nash Jr. — John Forbes Nash Pour les articles homonymes, voir John Nash. John Forbes Nash Jr en 2006 John Forbes Nash Jr (né le … Wikipédia en Français
Théorème de Kruskal — En mathématiques, le théorème des arbres de Kruskal est un résultat de théorie des graphes conjecturé en 1937 par Andrew Vázsonyi et démontré indépendamment en 1960 par Joseph Kruskal et S. Tarkowski[1], affirmant que l ensemble des arbres… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de plongement de nash