Théorème de müntz
- Théorème de müntz
-
Théorème de Müntz
Le théorème de l'approximation de Müntz–Szász est un résultat basique de la théorie de l'approximation qui a été découvert par Herman Müntz en 1914 puis par Otto Szász en 1916. Ce théorème avait été conjecturé sous cette forme par Sergeï Natanovitch Bernstein.
Soit I un segment de  , le théorème de Weierstrass assure que toute fonction continue de I dans
, le théorème de Weierstrass assure que toute fonction continue de I dans  est limite uniforme d'une suite de polynômes.
est limite uniforme d'une suite de polynômes.
Le théorème de Mûntz assure que, plus généralement, si une suite de réels distincts λn est telle que la série 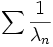 diverge, alors toute fonction continue sur I est limite uniforme d'une suite de combinaisons linéaires des fonctions
diverge, alors toute fonction continue sur I est limite uniforme d'une suite de combinaisons linéaires des fonctions 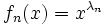 .
.
 Portail des mathématiques
Portail des mathématiques
Catégories : Analyse réelle | Analyse fonctionnelle | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de müntz de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Theoreme de Muntz — Théorème de Müntz Le théorème de l approximation de Müntz–Szász est un résultat basique de la théorie de l approximation qui a été découvert par Herman Müntz en 1914 puis par Otto Szász en 1916. Ce théorème avait été conjecturé sous cette forme… … Wikipédia en Français
Théorème de Müntz — Le théorème de Müntz Szász est un résultat basique de la théorie de l approximation qui a été découvert par Herman Müntz (en) en 1914 puis par Otto Szász (en) en 1916. Ce théorème avait été conjecturé sous cette forme par Sergeï… … Wikipédia en Français
Müntz — Théorème de Müntz Le théorème de l approximation de Müntz–Szász est un résultat basique de la théorie de l approximation qui a été découvert par Herman Müntz en 1914 puis par Otto Szász en 1916. Ce théorème avait été conjecturé sous cette forme… … Wikipédia en Français
Muntz — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Muntz est un nom de famille notamment porté par : Eugène Müntz (1845 1902), un historien de l art français. Herman Müntz (en) (1884 1956),… … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… … Wikipédia en Français
Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
 , le théorème de Weierstrass assure que toute fonction continue de I dans
, le théorème de Weierstrass assure que toute fonction continue de I dans  est limite uniforme d'une suite de polynômes.
est limite uniforme d'une suite de polynômes.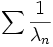 diverge, alors toute fonction continue sur I est limite uniforme d'une suite de combinaisons linéaires des fonctions
diverge, alors toute fonction continue sur I est limite uniforme d'une suite de combinaisons linéaires des fonctions 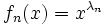 .
.