Théorème de lusin

Théorème de lusin

Théorème de Lusin

En mathématiques, le théorème de Lusin ou Luzin (d'après Nikolai Luzin) est pour l'analyse réelle, un autre forme du second principe de Littlewood.

Il énonce que toute fonction mesurable est continue sur une grande partie de son domaine de définition.

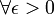Pour un intervalle [a,b], soit f:[a,b]\rightarrow \mathbb{C} une fonction mesurable. Alors \forall \epsilon > 0, il existe un compact E \subset [a,b] tel que la restriction à E de f est continue et μ(Ec) < ε, où Ec représente le complémentaire of E. Noter que E hérite de la topologie de [a,b], et dans le cadre de cette topologie, on peut définir la continuité de f restreinte à E.

Voici une preuve simple. On rappelle que les fonctions continues sont denses dans L1([a,b]). Alors, il existe une suite de fonctions continues {gn} telle que 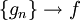\{ g_n\} \rightarrow f dans L1. De cette suite, on peut extraire une sous-suite 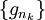\{ g_{n_k}\} telle que 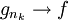g_{n_k} \rightarrow f presque partout. En utilisant le théorème d'Egoroff, on a 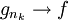g_{n_k} \rightarrow f en convergence uniforme sauf sur un ensemble de mesure aussi faible que voulue. Comme l'ensemble des fonctions continues est fermée par convergence uniforme, cela termine la démonstration.

Bibliographie

  • Walter Rudin, Analyse réelle et complexe : cours et exercices [détail des éditions]
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Lusin ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de lusin de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Théorème de Lusin — En mathématiques, le théorème de Lusin ou Luzin (d après Nikolai Luzin) est pour l analyse réelle, un autre forme du second principe de Littlewood. Il énonce que toute fonction mesurable est continue sur une grande partie de son domaine de… …   Wikipédia en Français

  • Théorème de Luzin — Théorème de Lusin En mathématiques, le théorème de Lusin ou Luzin (d après Nikolai Luzin) est pour l analyse réelle, un autre forme du second principe de Littlewood. Il énonce que toute fonction mesurable est continue sur une grande partie de son …   Wikipédia en Français

  • Theoreme d'Egoroff — Théorème d Egoroff Le théorème d’Egoroff, nommé ainsi en hommage à Dimitri Egoroff, un phycisien et géomètre russe, établit une condition de convergence uniforme dans certains espaces mesurables. Ce théorème peut servir en particulier à montrer… …   Wikipédia en Français

  • Lusin — Nikolaï Louzine Photo d archive de Nikolaï N. Louzine. Nikolaï Nikolaïevitch Louzine (en russe : Николай Николаевич Лузин, autres orthographes : Lusin ou Luzin), né le 9 décembre 1883 à Irkoutsk et mort le 28 janvier 1950 à …   Wikipédia en Français

  • Théorème d'Egoroff — Le théorème d’Egoroff, nommé ainsi en hommage à Dimitri Egoroff, un physicien et géomètre russe, établit une condition de convergence uniforme dans certains espaces mesurables. Ce théorème peut servir en particulier à montrer le théorème de Lusin …   Wikipédia en Français

  • Nikolai Lusin — Nikolaï Louzine Photo d archive de Nikolaï N. Louzine. Nikolaï Nikolaïevitch Louzine (en russe : Николай Николаевич Лузин, autres orthographes : Lusin ou Luzin), né le 9 décembre 1883 à Irkoutsk et mort le 28 janvier 1950 à …   Wikipédia en Français

  • Nikolaï Nikolaïevitch Lusin — Nikolaï Louzine Photo d archive de Nikolaï N. Louzine. Nikolaï Nikolaïevitch Louzine (en russe : Николай Николаевич Лузин, autres orthographes : Lusin ou Luzin), né le 9 décembre 1883 à Irkoutsk et mort le 28 janvier 1950 à …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”