Théorème de liouville (variable complexe)

Théorème de Liouville (variable complexe)

Pour les articles homonymes, voir Théorème de Liouville.

Joseph Liouville.

En analyse complexe, le théorème de Liouville est un résultat portant sur les fonctions entières (les fonctions holomorphes sur tout le plan complexe). Alors qu'il existe un grand nombre (infinité non dénombrable) de fonctions infiniment dérivables et bornées sur la droite réelle, le théorème de Liouville affirme que toute fonction entière bornée est constante.

Énoncé

Le théorème de Liouville s'énonce ainsi :

Théorème de Liouville — Si f est une fonction définie et holomorphe sur le plan complexe, alors f est constante dès lors qu'elle est bornée.

Ce théorème peut être amélioré:

Théorème — Si f est une fonction entière à croissance polynomiale de degré au plus k, au sens où:

$\exists (A,B)\in (\R_+)^2,\ \forall z\in \mathbb{C},\quad |f(z)|\leq A+B|z|^k$

alors f est une fonction polynomiale de degré inférieur ou égal à k.

Démonstration

La démonstration proposée, relativement courte, s'appuie sur l'inégalité de Cauchy. D'autres démonstrations possibles reposent indirectement sur la formule intégrale de Cauchy^[1].

Premier énoncé

Soit une fonction entière f, qui soit bornée sur C. Dans ce cas, il existe un majorant M du module de f. L'inégalité de Cauchy s'applique à f et à tout disque de centre z et de rayon R ; elle donne:

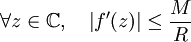$\forall z\in \mathbb{C},\quad \left|f'(z)\right|\leq \frac{M}{R}$ .

Si on fixe z et qu'on fait tendre R vers l'infini, il vient:

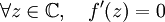$\forall z\in \mathbb{C},\quad f'(z)=0$ .

Par conséquent, la dérivée de f est partout nulle, donc f est constante.

Second énoncé

On suppose que la fonction entière f est à croissance polynomiale. L'inégalité de Cauchy est de nouveau appliquée au disque de centre z et de rayon R:

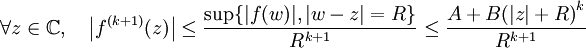$\forall z\in \mathbb{C},\quad \left|f^{(k+1)}(z)\right|\leq \frac{\sup\{|f(w)|,|w-z|=R\}}{R^{k+1}}\leq \frac{A+B { \left(|z|+R\right)}^k}{R^{k+1}}$ .

À nouveau, en faisant tendre R vers l'infini, il vient:

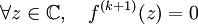
$\forall z\in \mathbb{C},\quad f^{(k+1)}(z)=0$

Par intégrations successives, la fonction f est une fonction polynomiale en z et son degré est inférieur ou égal à k.

Le théorème peut être démontré en utilisant la formule intégrale de Cauchy pour montrer que la dérivée complexe de f est identiquement nulle, mais ce n'est pas ainsi que Liouville l'a démontré ; et plus tard Cauchy disputa à Liouville la paternité du résultat. L'Histoire a cependant jugé qu'il n'y avait pas là manifestation de la loi de Stigler : Cauchy aurait pu facilement le démontrer avant Liouville mais ne l'a pas fait.

Le théorème est considérablement amélioré par le petit théorème de Picard, qui énonce que toute fonction entière non bornée prend tous les nombres complexes comme valeurs, à l'exception d'au plus un point.

Applications

Théorème de d'Alembert-Gauss

Article détaillé : Théorème de d'Alembert-Gauss.

Le théorème de d'Alembert-Gauss (ou encore théorème fondamental de l'algèbre) affirme que tout polynôme complexe admet une racine. Autrement dit, le corps des nombres complexes est algébriquement clos. Ce théorème peut être démontré en utilisant des outils d'analyse, et en particulier le théorème de Liouville énoncé ci-dessus, voir l'article détaillé pour la preuve.

Etude de la sphère de Riemann

En termes de surface de Riemann, le théorème peut être généralisé de la manière suivante: si $M$ est une surface de Riemann parabolique (le plan complexe par exemple) et si $N$ est une surface hyperbolique (un disque ouvert par exemple), alors toute fonction holomorphe $f : M \to N$ doit être constante.

Fonctions elliptiques

Article détaillé : Fonction elliptique.

Il est aussi utilisé pour établir qu'une fonction elliptique sans pôles est forcément constante ; c'est d'ailleurs cela que Liouville avait primitivement établi.

Notes et références

↑ Voir par exemple la preuve donnée dans Rudin, p.254, quelque peu différente.

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Liouville (variable complexe) ».

Catégories : Théorème de mathématiques | Analyse complexe

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de liouville (variable complexe) de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Theoreme de Liouville (variable complexe) — Théorème de Liouville (variable complexe) Pour les articles homonymes, voir Théorème de Liouville. Joseph Liouville. En analyse complexe, le thé … Wikipédia en Français
Théorème de Liouville (variable complexe) — Pour les articles homonymes, voir Théorème de Liouville. Joseph Liouville. En analyse complexe, le théorème de Liouville est un résultat portant sur les fonctions entière … Wikipédia en Français
Variable complexe — Analyse complexe L analyse complexe est le domaine des mathématiques étudiant les fonctions holomorphes, c est à dire les fonctions définies sur un certain domaine du plan complexe, prenant des valeurs complexes, et qui sont dérivables en tant… … Wikipédia en Français
Théorème de d'Alembert — Gauss Pour les articles homonymes, voir Théorème de Gauss. Jean le Rond D Alembert est le premier à ressentir la nécessité de démontrer le th … Wikipédia en Français
Théorème de d’Alembert-Gauss — Théorème de d Alembert Gauss Pour les articles homonymes, voir Théorème de Gauss. Jean le Rond D Alembert est le premier à ressentir la nécessité de démontrer le th … Wikipédia en Français
Théorème fondamental de l'algèbre — Théorème de d Alembert Gauss Pour les articles homonymes, voir Théorème de Gauss. Jean le Rond D Alembert est le premier à ressentir la nécessité de démontrer le th … Wikipédia en Français
Théorème de d'Alembert-Gauss — Pour les articles homonymes, voir Théorème de Gauss. Jean le Rond D Alembert est le premier à ressentir la nécessité de démontrer le théorème fondamental de l algèbre. Sa motivation est entièrement analytique, il r … Wikipédia en Français
FONCTIONS ANALYTIQUES - Fonctions d’une variable complexe — On se propose, dans ce premier article, d’exposer, avec des démonstrations quasiment complètes, les résultats les plus élémentaires de la théorie des fonctions analytiques d’une variable complexe; les deux derniers chapitres sont consacrés à… … Encyclopédie Universelle
LIOUVILLE (J.) — Joseph Liouville fut un bon artisan des mathématiques, déployant une activité considérable dans l’enseignement et la diffusion des idées mathématiques de son temps; il est le fondateur du Journal de mathématiques pures et appliquées appelé… … Encyclopédie Universelle
Theoreme d'Abel (algebre) — Théorème d Abel (algèbre) Pour les articles homonymes, voir Théorème d Abel. Niels Henrik Abel (1802 … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de liouville (variable complexe)