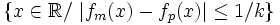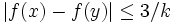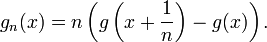Théorème de la limite simple de Banach

Théorème de la limite simple de Baire

En mathématiques, le théorème de la limite simple de Baire est un surprenant résultat d'analyse sur la continuité d'une limite simple d'une suite de fonctions continues. Il est nommé ainsi en l'honneur du mathématicien français René Baire. C'est une conséquence de la propriété de Baire.

Énoncé

Soit $(f n)$ une suite de fonctions continues de $\mathbb{R}$ dans $\mathbb{R}$ . Si elle converge simplement vers une fonction f, alors f est continue sur un ensemble dense de réels.

Démonstration

Pour tous entiers positifs $n$ et $k$ , on pose

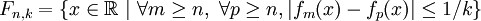$F_{n,k} = \{x\in \R\ |\ \forall m\geq n,\ \forall p \geq n, |f_m(x) - f_p(x)|\leq 1/k\}$ .

On note $I n, k$ l'intérieur de $F n, k$ . On note

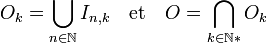$O_k = \bigcup_{n\in \mathbb N}I_{n,k}\quad \mathrm{et}\quad O = \bigcap_{k \in \mathbb N*} O_k$ .

On va prouver que $O$ est dense dans $\R$ et que $f$ est continue en tout point de $O$ .

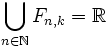1) $F n, k$ est un fermé et $\bigcup_{n\in \mathbb N}F_{n,k}= \R$ .

Pour tous entiers $m$ , $p$ et $k$ , les fonctions $f m$ et $f p$ sont continues donc l'ensemble

$\{x\in \R /\ |f_m(x) - f_p(x)|\leq 1/k\}$

est un fermé et $F n, k$ est fermé comme intersection de fermés.

Pour tout réel $x$ , la suite $(f n (x))$ converge simplement vers $f (x)$ . C'est donc une suite de Cauchy et il existe un entier n tel que

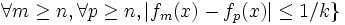$\forall m\geq n, \forall p \geq n, |f_m(x) - f_p(x)|\leq 1/k\}$ .

Ceci assure qu'il existe un entier $n$ tel que $x$ appartient à $F n, k$ .

2) Pour tout entier k, $O k$ est un ouvert dense dans $\R$ .

L'ensemble $O k$ est un ouvert car c'est une union d'ouverts. Pour montrer que $O k$ est dense dans $\R$ , il suffit de prouver que pour tout réel $x$ et pour tout réel positif $h$ , l'intervalle $[x - h; x + h]$ rencontre $O k$ .

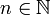On considère la suite dénombrable de fermés $F_{n,k} \cap [x - h; x + h]$ . Son union pour $n \in \N$ donne l'intervalle $[x - h; x + h]$ dont l'intérieur est non vide. Par la contraposée du théorème de Baire, on en déduit qu'il existe un entier $n$ tel que $F_{n,k} \cap [x - h; x + h]$ soit d'intérieur non vide (En effet, le propriété de Baire peut encore s'énoncer : une union dénombrable de fermés d'intérieurs vides est d'intérieur vide. Par contraposée, puisque l'union des fermés est d'intérieur non vide, il existe un fermé dont l'intérieur est non vide). Cela signifie que $[x - h, x + h]$ rencontre $I n, k$ donc rencontre $O k$ .

3) $O\,$ est dense dans $\R$ .

Par application immédiate du théorème de Baire, une intersection dénombrable d'ouverts denses dans $\R$ est dense dans $\R$ .

4) Pour tout réel $x$ de $O$ , $f$ est continue en $x$ .

Pour tout $x$ de $O$ , $x$ appartient à $O k$ pour tout entier $k$ . Donc pour tout entier $k$ , il existe un entier $n$ tel que $x$ appartient à $I n, k$ .

Pour tout $y$ de $I n, k$ et tout entier $p$ supérieur ou égal à $n$ , on a

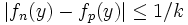$|f_n(y) - f_p(y)| \leq 1/k$ .

Par passage à la limite, on obtient

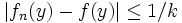$|f_n(y) - f(y)| \leq 1/k$ .

En particulier

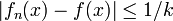$|f_n(x) - f(x)| \leq 1/k$ .

La fonction $f n$ étant continue en $x$ , il existe un ouvert $U$ contenant $x$ tel que, pour tout réel $y$ de $U$ , on ait

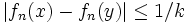$|f_n(x) - f_n(y)|\leq 1/k$ .

Donc, pour le réel x et pour tout réel $y$ de l'ouvert 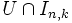$U \cap I_{n,k}$ , on a les trois inégalités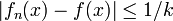

$|f_n(x) - f(x)| \leq 1/k$

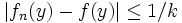
$|f_n(y) - f(y)| \leq 1/k$

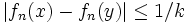$|f_n(x) - f_n(y)| \leq 1/k$ .

Par sommation, on obtient

$|f(x) - f(y)| \leq 3/k$

ce qui assure la continuité de $f$ en $x$ .

Exemple d'utilisation

Si une fonction 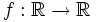$f:\R\to \R$ est une dérivée, c'est-à-dire qu'il existe 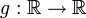$g:\R\to \R$ dérivable telle que $g' = f$ , alors $f$ est la limite simple de la suite de fonction $(g n)$ définie par

$g_n(x) = n\left(g\left(x + \frac{1}{n}\right) - g(x)\right).$

On en déduit donc que toute fonction dérivée est continue sur un ensemble dense de réels.

Liens et sources

[pdf] Lemme de Baire Par G. Godefroy.

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de la limite simple de Baire ».

Catégories : Théorème de mathématiques | Analyse réelle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de la limite simple de Banach de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Théorème de baire — Le théorème de Baire, dit aussi lemme de Baire, est un théorème de topologie dû au mathématicien René Baire. Un espace topologique est dit de Baire si toute intersection dénombrable d ouverts denses est dense. De façon équivalente, un espace… … Wikipédia en Français
Théorème de Baire — Le théorème de Baire, dit aussi lemme de Baire, est un théorème de topologie dû au mathématicien René Baire. Un espace topologique est dit de Baire si toute intersection dénombrable d ouverts denses est dense. De façon équivalente, un espace… … Wikipédia en Français
Theoreme de Riemann-Lebesgue — Théorème de Riemann Lebesgue En analyse, le théorème de Riemann Lebesgue, parfois aussi appelé lemme de Riemann Lebesgue (ou encore lemme intégral de Riemann Lebesgue) est un résultat de théorie de Fourier. Il apparaît sous deux formes… … Wikipédia en Français
Théorème de riemann-lebesgue — En analyse, le théorème de Riemann Lebesgue, parfois aussi appelé lemme de Riemann Lebesgue (ou encore lemme intégral de Riemann Lebesgue) est un résultat de théorie de Fourier. Il apparaît sous deux formes différentes selon que l on s intéresse… … Wikipédia en Français
Théorème de Riemann-Lebesgue — En analyse, le théorème de Riemann Lebesgue, parfois aussi appelé lemme de Riemann Lebesgue (ou encore lemme intégral de Riemann Lebesgue) est un résultat de théorie de Fourier. Il apparaît sous deux formes différentes selon que l on s intéresse… … Wikipédia en Français
Theoreme de Cauchy-Lipschitz — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Théorème de Picard-Lindelöf — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Théorème de cauchy-lipschitz — Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Theoreme de projection sur un convexe ferme — Théorème de projection sur un convexe fermé En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace… … Wikipédia en Français
Théorème de projection orthogonale sur un convexe — Théorème de projection sur un convexe fermé En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de la limite simple de Banach

Théorème de la limite simple de Baire

Énoncé

Exemple d'utilisation

Liens et sources

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Théorème de la limite simple de Banach

Théorème de la limite simple de Baire

Énoncé

Exemple d'utilisation

Liens et sources

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link