Théorème de goursat
- Théorème de goursat
-
Théorème de Goursat
Le théorème de Goursat, encore appelé lemme de Goursat est un résultat important de l'analyse complexe, puisqu'il est la cause directe des différents théorèmes de Cauchy.
Énoncé
Soit 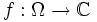 une fonction holomorphe sur un ouvert convexe
une fonction holomorphe sur un ouvert convexe 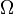 . Alors l'intégrale de Cauchy suivant tout triangle inclus dans
. Alors l'intégrale de Cauchy suivant tout triangle inclus dans 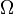 est nulle.
est nulle.
 Portail des mathématiques
Portail des mathématiques
Catégories : Analyse complexe | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de goursat de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Theoreme de Goursat — Théorème de Goursat Le théorème de Goursat, encore appelé lemme de Goursat est un résultat important de l analyse complexe, puisqu il est la cause directe des différents théorèmes de Cauchy. Énoncé Soit une fonction holomorphe sur un ouvert… … Wikipédia en Français
Théorème de Goursat — Le théorème de Goursat, encore appelé lemme de Goursat est un résultat important de l analyse complexe, puisqu il est la cause directe des différents théorèmes de Cauchy. Énoncé Soit une fonction holomorphe sur un ouvert convexe . Alors l… … Wikipédia en Français
Theoreme de Goursat et Levi-Civita — Théorème de Goursat et Levi Civita Le théorème est démontré par Goursat (1889) pour le bicentenaire des Principia. Tullio Levi Civita le reprendra (1903) pour des questions de perturbations en mécanique céleste. Il sera amplement repris et… … Wikipédia en Français
Théorème de goursat et levi-civita — Le théorème est démontré par Goursat (1889) pour le bicentenaire des Principia. Tullio Levi Civita le reprendra (1903) pour des questions de perturbations en mécanique céleste. Il sera amplement repris et développé par un article d Arnold et de… … Wikipédia en Français
Théorème de Goursat et Levi-Civita — Le théorème est démontré par Goursat (1889) pour le bicentenaire des Principia. Tullio Levi Civita le reprendra (1903) pour des questions de perturbations en mécanique céleste. Il sera amplement repris et développé par un article d Arnold et de… … Wikipédia en Français
Theoreme integral de Cauchy — Théorème intégral de Cauchy Pour les articles homonymes, voir Cauchy. En analyse complexe, le théorème intégral de Cauchy est un important résultat concernant les intégrales curvilignes de fonctions holomorphes dans le plan complexe. D après ce… … Wikipédia en Français
Théorème de Cauchy (surfaces de Riemann) — Théorème intégral de Cauchy Pour les articles homonymes, voir Cauchy. En analyse complexe, le théorème intégral de Cauchy est un important résultat concernant les intégrales curvilignes de fonctions holomorphes dans le plan complexe. D après ce… … Wikipédia en Français
Théorème intégral de cauchy — Pour les articles homonymes, voir Cauchy. En analyse complexe, le théorème intégral de Cauchy est un important résultat concernant les intégrales curvilignes de fonctions holomorphes dans le plan complexe. D après ce théorème, si deux chemins… … Wikipédia en Français
Theoreme de Bertrand — Théorème de Bertrand Le mathématicien Joseph Bertrand (1822 1900) démontra en 1873 (Compte Rendus de l Académie des Sciences, vol. 77, p.849) en mécanique du mouvement à force centrale le théorème suivant : seules les lois de force de… … Wikipédia en Français
Théorème de bertrand — Le mathématicien Joseph Bertrand (1822 1900) démontra en 1873 (Compte Rendus de l Académie des Sciences, vol. 77, p.849) en mécanique du mouvement à force centrale le théorème suivant : seules les lois de force de Hooke k.OM, qui… … Wikipédia en Français
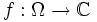 une fonction holomorphe sur un ouvert convexe
une fonction holomorphe sur un ouvert convexe 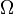 . Alors l'intégrale de Cauchy suivant tout triangle inclus dans
. Alors l'intégrale de Cauchy suivant tout triangle inclus dans 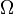 est nulle.
est nulle.