Théorème de clairaut (géométrie)
- Théorème de clairaut (géométrie)
-
Théorème de Clairaut (géométrie)
Le théorème de Clairaut en géométrie concerne des égalités d'aire entre parallélogrammes construits autour d'un triangle.
Enoncé
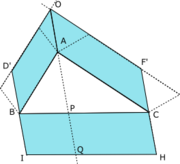
- Si ABC est un triangle
- Si ABDE et ACFG sont des parallélogrammes extérieurs au triangle
- Si (DE) et (FG) se coupent en O
- Si, enfin, BCHI est un parallélogramme extérieur au triangle tel que [OA] et [CH] soient parallèles de même longueur
alors
- L'aire du parallélogramme BCHI est égale à la somme des aires des deux autres parallélogrammes
Démonstration
Il suffit de déformer les parallélogrammes sans modifier leur aire.
Puisque OF'CA, CHIB, BD'OA sont des parallélogrames,"[OA] et [CH] soient parallèles de même longueur" implique que [BD'], [IB], [QP], [HC] et [CF'] y sont également parallèles de même longueur.
- aire(ABDE) =aire(ABD'O) (même base, même hauteur)
- aire(ACFG) = aire(ACF'O)
Si la droite OA rencontre (BC) et (HI) en P et Q alors
- aire(ABD'O) =aire(BIQP) (même base , même hauteur)
- aire(ACF'O) = aire(CHQP)
Cas particulier
Si ABC est un triangle rectangle en A, si ABDE et ACFG sont des carrés, alors BCHI est aussi un carré et il s'agit du théorème de Pythagore
Portail de la géométrie
Catégories : Théorème de mathématiques | Géométrie du triangle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de clairaut (géométrie) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème de Clairaut (géométrie) — Le théorème de Clairaut en géométrie concerne des égalités d aire entre parallélogrammes construits autour d un triangle. Enoncé Théorème de Clairaut Si ABC est un triangle Si ABDE et ACFG sont des parallélogrammes extérieurs au triangle Si (DE)… … Wikipédia en Français
Theoreme de Clairaut — Théorème de Clairaut Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Il existe trois théorèmes de Clairaut, du nom du mathématicien français Alexis Claude Clairaut : Le théorème de Clairaut, en… … Wikipédia en Français
Théorème de clairaut — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Il existe trois théorèmes de Clairaut, du nom du mathématicien français Alexis Claude Clairaut : Le théorème de Clairaut, en gravimétrie, qui relie… … Wikipédia en Français
Théorème de Clairaut — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Il existe trois théorèmes de Clairaut, du nom du mathématicien français Alexis Claude Clairaut : Le théorème de Clairaut, en gravimétrie, qui relie… … Wikipédia en Français
Theoreme de Pythagore — Théorème de Pythagore Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté… … Wikipédia en Français
Théorème de l'hypoténuse — Théorème de Pythagore Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté… … Wikipédia en Français
Théorème de pythagore — Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté opposé à l’angle droit)… … Wikipédia en Français
Théorème de Pythagore — Relation entre les longueurs des cô … Wikipédia en Français
Théorème de Clairault — Théorème de Clairaut Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Il existe trois théorèmes de Clairaut, du nom du mathématicien français Alexis Claude Clairaut : Le théorème de Clairaut, en… … Wikipédia en Français
GÉOMÉTRIE — La géométrie est communément définie comme la science des figures de l’espace. Cette définition un peu incertaine risque de conduire à inclure dans la géométrie des questions qui ne sont géométriques que dans leur langage, mais relèvent en fait… … Encyclopédie Universelle
Théorème de Clairaut
Preuve
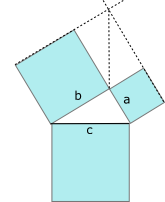Clairaut et Pythagore
