- Théorème de Sylvester
-
Loi d'inertie de Sylvester
La loi d'inertie de Sylvester est un théorème de classification des formes quadratiques sur un espace vectoriel réel de dimension finie.
Soit
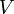 un espace vectoriel sur
un espace vectoriel sur 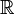 de dimension n, et
de dimension n, et 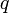 une forme quadratique de rang r. Il existe un entier
une forme quadratique de rang r. Il existe un entier 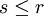 et des formes linéaires indépendantes
et des formes linéaires indépendantes 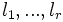 telles que
telles que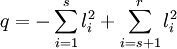
.
Cette écriture n'est pas unique, mais l'entier s n'en dépend pas. On l'appelle l'indice de
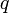 .
.Deux formes quadratiques sur
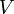 sont équivalentes si et seulement si elles ont même rang et même indice.
sont équivalentes si et seulement si elles ont même rang et même indice.
Preuve.Le théorème de réduction de Gauss assure de l'existence de r des formes linéaires indépendantes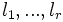 et de réels
et de réels  tous non nuls tels que
tous non nuls tels que 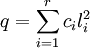 . L'existence de la décomposition annoncée s'obtient en renumérotant les
. L'existence de la décomposition annoncée s'obtient en renumérotant les 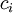 de façon à mettre en premier ceux qui sont strictement négatifs, puis en remplaçant
de façon à mettre en premier ceux qui sont strictement négatifs, puis en remplaçant 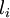 par
par 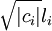 .
.Pour montrer que s ne dépend que de q, montrons que c'est le maximum des dimensions des sous-espaces sur lesquels q est définie négative. (On montrerait de même que r-s est le maximum des dimensions des sous-espaces sur lesquels q est définie positive). Soient
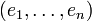 une base de
une base de 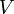 dans laquelle
dans laquelle 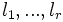 sont les r premières fonctions coordonnées (en particulier,
sont les r premières fonctions coordonnées (en particulier, 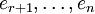 est une base du radical
est une base du radical 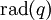 de
de 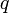 ), et
), et 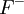 (resp.
(resp.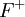 ) le sous-espace engendré par
) le sous-espace engendré par  (resp.
(resp.  ). On obtient une décomposition
). On obtient une décomposition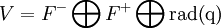
en somme directe de sous-espaces deux à deux orthogonaux pour la forme bilinéaire associée à
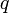 , la restriction de
, la restriction de 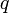 à
à 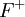 (resp.
(resp.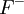 ) étant définie positive (resp. définie négative). Soit
) étant définie positive (resp. définie négative). Soit 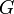 un sous-espace de dimension m sur lequel
un sous-espace de dimension m sur lequel 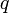 est définie négative. Comme
est définie négative. Comme 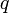 est définie positive sur
est définie positive sur 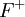 , ces deux sous-espaces sont en somme directe et
, ces deux sous-espaces sont en somme directe et 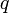 est non dégénérée sur cette somme, donc
est non dégénérée sur cette somme, donc 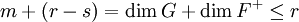 , c'est-à-dire
, c'est-à-dire 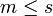 .
.Passons maintenant au critère d'équivalence. Si
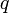 est une forme quadratique s'écrivant
est une forme quadratique s'écrivant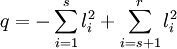
,
et si
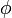 est une application linéaire inversible, on a
est une application linéaire inversible, on a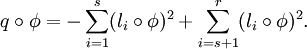
Les formes
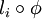 sont indépendantes si les
sont indépendantes si les 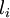 le sont, donc
le sont, donc 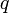 et
et 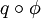 ont même indice (on sait déjà d'après la théorie générale qu'elles ont même rang). Réciproquement, si
ont même indice (on sait déjà d'après la théorie générale qu'elles ont même rang). Réciproquement, si 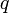 et
et 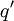 ont même indice et même rang, elles ont même matrice par rapport à des bases convenables et sont donc bien équivalentes.
ont même indice et même rang, elles ont même matrice par rapport à des bases convenables et sont donc bien équivalentes.Liens internes
- Portail des mathématiques
Catégorie : Algèbre bilinéaire
Wikimedia Foundation. 2010.
