Théorème de Miquel

Théorème de Miquel

En géométrie plane, les théorèmes de Miquel sont des théorèmes concernant des cercles concourants.

Les énoncés

Théorème des trois cercles

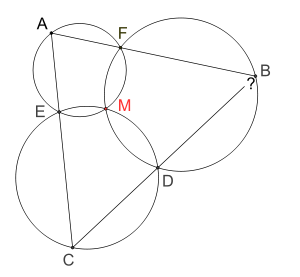
Soient trois cercles (C1), (C2), (C3) se rencontrant en un point M, on appelle D, E et F les autres points d'intersection des cercles (C2) et (C3), (C3) et (C1), (C1) et (C2). Soit A un point de (C1) tel que la droite (FA) recoupe (C2) en B et la droite (EA) recoupe (C3) en C. Le théorème de Miquel affirme alors que les points B, D et C sont alignés.

Réciproque : si ABC est un triangle, et si D, E et F sont trois points situés respectivement sur (BC), (CA) et (AB) alors les cercles circonscrits aux triangles (AEF), (BDF) et (CDE) se rencontrent en un point M.
Miquel1bis.svg
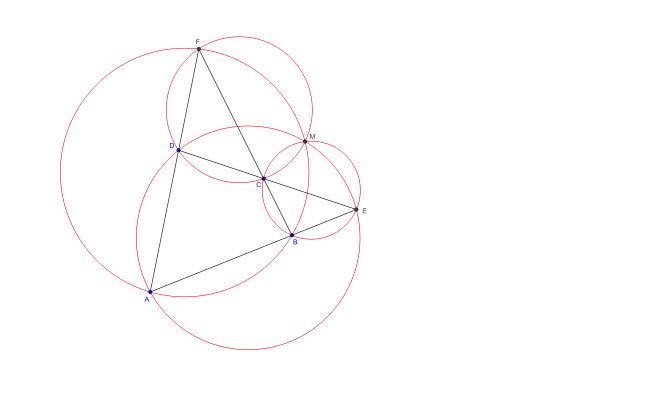
Théorème du quadrilatère complet

Si ABCDEF est un quadrilatère complet alors les cercles circonscrits aux triangles (EAD), (EBC), (FAB) et (FDC) sont concourants en un point M appelé point de Miquel.

Démontré en 1838 par A. Miquel, ce résultat fut dénommé théorème du pivot par Forder.

Point miquel.svg
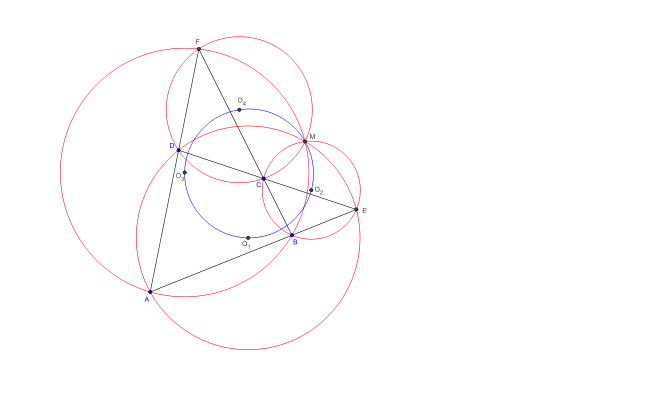
Cercle de Miquel

Les centres O1, O2, O3, O4 des quatre cercles et le point de Miquel M sont cocycliques.

Le cercle contenant ces cinq points est dit cercle de Miquel

Cercle miquel.svg
Théorème des quatre cercles

Si (C1), (C2),(C3) et (C4) sont quatre cercles, si A1 et B1 sont les intersections de (C1) et (C2), A2 et B2 les points d'intersection de (C2) et (C3), A3 et B3 les intersections de (C3) et (C4) et A4 et B4 les intersections de (C1) et (C4), les points A1, A2, A3, A4 sont alignés ou cocycliques si et seulement s'il en est de même des points B1, B2, B3, B4.

Miquel2.svg Miquel3.svg
Théorème du sixième cercle

Si ABCDE est un pentagone quelconque. Si F, G, H, I, J sont les points d'intersection des côtés (EA) et (BC) , (AB) et (CD), (BC) et (DE), (CD) et (EA), (DE) et (AB), alors les points d'intersection des cinq cercles circonscrits à (ABF), (BCG), (CDH), (DEI), (EAJ) sont situés sur un sixième cercle qui contient aussi les centres des cinq cercles précédents.

Réciproque
Théorème des cinq cercles : si (C1), (C2), (C3), (C4), (C5) sont cinq cercles dont les centres sont sur un cercle (C) et qui se coupent entre voisins sur (C) alors les cinq droites joignant les points d'intersection non situés sur (C) d'un cercle avec ses voisins se rencontrent sur les cercles.
Miquel4.svg

Remarques historiques

Auguste Miquel a publié une partie de ces théorèmes dans les cahiers de Liouville (Journal de mathématiques pures et appliquées) en 1838.

Le premier théorème de Miquel est un résultat classique connu bien avant lui utilisant le théorème de l'angle inscrit.

Le nom de point de Miquel est attribué au point de concours des quatre cercles d'un quadrilatère complet mais la propriété était connue déjà par Jakob Steiner (1828) et même probablement par William Wallace.

Le théorème des cinq cercles (ou du sixième cercle) est un cas particulier d'un théorème général énoncé et démontré par le mathématicien William Kingdon Clifford. Ce problème est revenu au goût du jour suite à un défi lancé en 2002 par le président chinois Jiang Zemin lors d'un congrès de mathématiciens à Pékin en 2002. Il fut repris par Alain Connes lors d'un séminaire en octobre 2002.

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Miquel de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Theoreme de Miquel — Théorème de Miquel En géométrie plane, les théorèmes de Miquel sont des théorèmes concernant des cercles concourants. Les énoncés Théorème des trois cercles : Soient trois cercles (C1), (C2), (C3) se rencontrant en un point O, on appelle M,… …   Wikipédia en Français

  • Théorème de miquel — En géométrie plane, les théorèmes de Miquel sont des théorèmes concernant des cercles concourants. Les énoncés Théorème des trois cercles : Soient trois cercles (C1), (C2), (C3) se rencontrant en un point O, on appelle M, N et P les autres… …   Wikipédia en Français

  • Théorème du pivot — Théorème de Miquel En géométrie plane, les théorèmes de Miquel sont des théorèmes concernant des cercles concourants. Les énoncés Théorème des trois cercles : Soient trois cercles (C1), (C2), (C3) se rencontrant en un point O, on appelle M,… …   Wikipédia en Français

  • Theoreme de l'angle inscrit et de l'angle au centre — Théorème de l angle inscrit et de l angle au centre Figure 1 : angles inscrits AMB = ANB et angle au centre AOB En géométrie euclidienne plane, plus précisément dans la géométrie du cercle, les théorèmes de l angle inscrit et de l angle au… …   Wikipédia en Français

  • Théorème de l'angle inscrit — et de l angle au centre Figure 1 : angles inscrits AMB = ANB et angle au centre AOB En géométrie euclidienne plane, plus précisément dans la géométrie du cercle, les théorèmes de l angle inscrit et de l angle au centre établissent des… …   Wikipédia en Français

  • Théorème de l'angle inscrit et de l'angle au centre — Figure 1 : angles inscrits AMB = ANB et angle au centre AOB En géométrie euclidienne plane, plus précisément dans la géométrie du cercle, les théorèmes de l angle inscrit et de l angle au centre établissent des relations liant les angles… …   Wikipédia en Français

  • Théorème du point fixe de Brouwer — En 1886 Henri Poincaré démontre un résultat équivalent au théorème du point fixe de Brouwer. L énoncé exact est prouvé pour la dimension trois par Piers Bohl pour la première fois en 1904, puis par Jacques Hadamard dans le cas général en 1910.… …   Wikipédia en Français

  • Theoreme de Schruttka — Point de Fermat Le point de Fermat, du nom du mathématicien français Pierre de Fermat est un point remarquable d un triangle en géométrie euclidienne. Il est également appelé point de Torricelli, son existence correspond au théorème de Schruttka… …   Wikipédia en Français

  • Théorème de Schruttka — Point de Fermat Le point de Fermat, du nom du mathématicien français Pierre de Fermat est un point remarquable d un triangle en géométrie euclidienne. Il est également appelé point de Torricelli, son existence correspond au théorème de Schruttka… …   Wikipédia en Français

  • Théorème de schruttka — Point de Fermat Le point de Fermat, du nom du mathématicien français Pierre de Fermat est un point remarquable d un triangle en géométrie euclidienne. Il est également appelé point de Torricelli, son existence correspond au théorème de Schruttka… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”