Theoreme de Schruttka
- Theoreme de Schruttka
-
Point de Fermat
Le point de Fermat, du nom du mathématicien français Pierre de Fermat est un point remarquable d'un triangle en géométrie euclidienne. Il est également appelé point de Torricelli, son existence correspond au théorème de Schruttka (aussi connu sous le nom de théorème de Torricelli, ou théorème de Fermat).
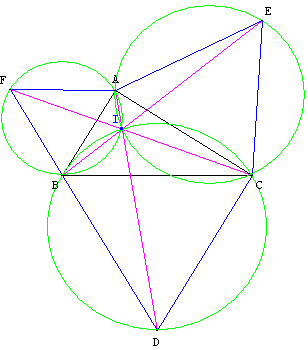
Construction du point de Fermat.
Point de Fermat — Soit ABC un triangle dont les angles sont inférieurs à 120°. Il existe un et un seul point I, dont la somme IA + IB + IC des distances aux trois sommets est minimale. Ce point est appelé point de Fermat.
Historique
L'existence d'un point minimisant la somme des distances à trois points distincts tire son origine d'un problème que Fermat posa à Toricelli (d'où les différentes appellations). Toricelli résolut ce problème d'une manière similaire à celle de Fermat, à l'aide des cercles circonscrits aux triangles équilatéraux issus des côtés du triangle initial, ces cercles sont les cercles de Torricelli. La démonstration fut rapportée par Viviani, pupille de Toricelli, en 1659[1].
Propriétés de ce point remarquable
- Les droites (IA), (IB) et (IC) forment entre elles des angles de 120°.
- Si ABC est bordé extérieurement par trois triangles équilatéraux BCD, ACE et ABF, les segments [AD], [BE] et [CF] sont concourants en I.
- Les cercles de Torricelli, circonscrits aux triangles BCD, ACE et ABF sont concourants en I (application du théorème du pivot de Forder démontré par Auguste Miquel en 1838).
Références
- ↑ (en) Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, 1929, p.221-222.
Portail de la géométrie
Catégories : Théorème de géométrie | Géométrie du triangle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Schruttka de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème de Schruttka — Point de Fermat Le point de Fermat, du nom du mathématicien français Pierre de Fermat est un point remarquable d un triangle en géométrie euclidienne. Il est également appelé point de Torricelli, son existence correspond au théorème de Schruttka… … Wikipédia en Français
Théorème de schruttka — Point de Fermat Le point de Fermat, du nom du mathématicien français Pierre de Fermat est un point remarquable d un triangle en géométrie euclidienne. Il est également appelé point de Torricelli, son existence correspond au théorème de Schruttka… … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… … Wikipédia en Français
Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Point de Fermat — Le point de Fermat, du nom du mathématicien français Pierre de Fermat est un point remarquable d un triangle en géométrie euclidienne. Il est également appelé point de Torricelli, son existence correspond au théorème de Schruttka (aussi connu… … Wikipédia en Français
