Théorème de Lehman Scheffer

Le théorème de Lehman-Scheffé a une importance particulière en statistiques puisqu'il permet de trouver des estimateurs sans biais optimaux qui ne peuvent pas être améliorés en termes de précision.

De tels estimateurs n'existent pas forcément mais si l'on dispose d'une statistique qui soit à la fois exhaustive et totale et d'un estimateur δ qui soit sans biais alors l'estimateur augmenté 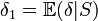est optimal et l'on ne peut pas trouver de meilleur estimateur sans biais.

Ce théorème nous donne donc une condition suffisante pour trouver un estimateur sans biais optimal. Il nous dit également que cet estimateur s'exprime comme une fonction de la statistique exhaustive totale S, c'est-à-dire de la forme g(S) où g est une fonction mesurable.

(On dit qu'une statistique est totale si: 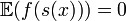implique f=0 presque partout)

• Portail des probabilités et des statistiques