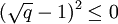Théorème de Hasse sur les courbes elliptiques
- Théorème de Hasse sur les courbes elliptiques
-
Théorème de Hasse
En mathématiques, le théorème de Hasse sur les courbes elliptiques limite le nombre de points d'une courbe elliptique sur un corps fini, au-dessus et en-dessous.
Si N est le nombre de points d'une courbe elliptique E sur un corps fini à q éléments, alors le résultat d'Helmut Hasse énonce que
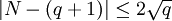 .
.
Ceci a été une conjecture d'Emil Artin. Ceci est équivalent à la détermination de la valeur absolue des racines des fonctions zeta locales de E.
L'interpretation est la suivante : N diffère de q + 1, le nombre de points de la droite projective sur le même corps, par un 'terme d'erreur' qui est la somme de deux nombres complexes, chacun de valeur absolue 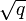 .
.
En fixant N = 0, on trouve
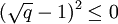
ce qui ne peut pas arriver, puisque q > 1. Par conséquent, N > 0 et il existe toujours au moins un point.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Corps fini | Théorie algébrique des nombres | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Hasse sur les courbes elliptiques de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème de hasse — En mathématiques, le théorème de Hasse sur les courbes elliptiques limite le nombre de points d une courbe elliptique sur un corps fini, au dessus et en dessous. Si N est le nombre de points d une courbe elliptique E sur un corps fini à q… … Wikipédia en Français
Théorème de Hasse — En mathématiques, le théorème de Hasse sur les courbes elliptiques limite le nombre de points d une courbe elliptique sur un corps fini, au dessus et en dessous. Si N est le nombre de points d une courbe elliptique E sur un corps fini à q… … Wikipédia en Français
Courbes Elliptiques — Courbe elliptique Une sélection de courbes cubiques réelles définies par l équation y2 = x3 + ax + b.. La région montrée est [ 3,3]². La courbe pour a=b=0 n est pas elliptique. En mathématiques, une courbe elliptique est un cas particulier de… … Wikipédia en Français
Courbes elliptiques — Courbe elliptique Une sélection de courbes cubiques réelles définies par l équation y2 = x3 + ax + b.. La région montrée est [ 3,3]². La courbe pour a=b=0 n est pas elliptique. En mathématiques, une courbe elliptique est un cas particulier de… … Wikipédia en Français
Helmut Hasse — Pour les articles homonymes, voir Hasse. Helmut Hasse Helmut Hasse est un mathématicien allemand né le 25 août 1898 à Kassel et mort le 26 décembre 1979 à Ahrensburg. Il … Wikipédia en Français
Theoreme de Taniyama-Shimura — Conjecture de Shimura Taniyama Weil La conjecture de Shimura Taniyama Weil énonce que, pour toute courbe elliptique sur , il existe une forme modulaire de poids 2 pour un sous groupe de congruence Γ0(N), ayant même fonction L que la courbe… … Wikipédia en Français
Théorème de Taniyama-Shimura — Conjecture de Shimura Taniyama Weil La conjecture de Shimura Taniyama Weil énonce que, pour toute courbe elliptique sur , il existe une forme modulaire de poids 2 pour un sous groupe de congruence Γ0(N), ayant même fonction L que la courbe… … Wikipédia en Français
Théorème de taniyama-shimura — Conjecture de Shimura Taniyama Weil La conjecture de Shimura Taniyama Weil énonce que, pour toute courbe elliptique sur , il existe une forme modulaire de poids 2 pour un sous groupe de congruence Γ0(N), ayant même fonction L que la courbe… … Wikipédia en Français
Conjectures de Weil — En mathématiques, les conjectures de Weil, qui sont devenues des théorèmes en 1974, ont été des propositions très influentes à la fin des années 1940 énoncées par André Weil sur les fonctions génératrices (connues sous le nom de fonctions zêta… … Wikipédia en Français
Conjectures De Weil — En mathématiques, les conjectures de Weil, qui sont devenues des théorèmes en 1974, ont été des propositions très influentes à la fin des années 1940 énoncées par André Weil sur les fonctions génératrices (connues sous le nom de fonctions zêta… … Wikipédia en Français
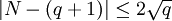 .
.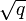 .
.