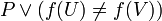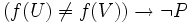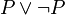- Théorème de Goodman-Myhill
-
Théorème de Diaconescu
Le théorème de Diaconescu, ou le théorème de Goodman-Myhill, énonce qu'une forme du principe du tiers exclu, qui est rejeté dans les mathématiques constructives, est la conséquence du controversé axiome du choix dans la théorie des ensembles. Ce fut découvert en 1975 par Diaconescu[1] et ensuite par Goodman et Myhill[2].
Preuve
Soit P une proposition quelconque. On construit les ensembles
Cette construction est possible selon l'axiome de séparation. Notons que dans la théorie classique, U et V seraient simplement
mais ces équivalences sont fondées sur le principe du tiers exclu, sans lequel on n'affirme pas «P ou ¬P».
L'axiome du choix affirme l'existence d'une fonction de choix f pour l'ensemble {U,V}, c'est à dire qu'il existe un f tel que
et par la construction de ces deux ensembles, celà signifie que
et, puisque 0≠1,
Mais si la proposition P était vraie, les deux ensembles U et V contiendraient 0 et 1, et l'axiome d'extensionnalité des ensembles affirme que dans ce cas, U et V seraient égaux, et que f(U) = f(V). Alors par contraposition
Enfin donc
Celà prouve que l'axiome du choix implique la loi du tiers exclu pour toutes propositions auxquelles s'applique l'axiome de séparation. La théorie classique des ensembles accepte cette axiome sans restriction, mais pour le constructivisme ce n'est pas acceptable dans sa forme générale à cause de son imprédicativité. Néanmoins la théorie constructive des ensembles accepte une version prédicative de cette axiome. Bien que la forme possible de la proposition P est limitée[3], et la preuve donne donc une forme limitée de la loi du tiers exclu, cette forme de la loi est toujours rejetée par les constructivistes, donc ils ne peuvent pas accepter la forme générale de l'axiome du choix non plus.
L'extensionnalité des ensembles est essentielle à cette démonstration; dans la théorie constructive des types ils ne sont pas nécessairement extensionelles. On peut parfois donner une preuve constructive de l'axiome du choix pour des types, mais à cause de la nature de ces types il s'agit de formes restreintes de l'axiome, par exemple l'axiome du choix dénombrable, voire dépendant.
Notes
- ↑ (en) R. Diaconescu, "Axiom of choice and complementation", Proceedings of the American Mathematical Society 51:176-178 (1975)
- ↑ (en) N. D. Goodman et J. Myhill, “Choice Implies Excluded Middle”, Zeitschrift fur Mathematische Logik und Grundlaaen der Mathematik 24:461 (1975)
- ↑ Wikipédia anglais décrit ces restrictions -- traduction pas encore effectuée
Catégorie : Théorie des ensembles
Wikimedia Foundation. 2010.

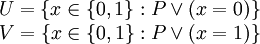
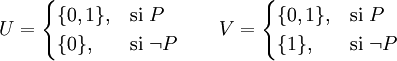
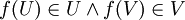
![[P \vee (f(U) = 0)] \wedge [P \vee (f(V) = 1)]](/pictures/frwiki/102/fe903b966555c7c17590ac64fd4dd3e1.png)