Théorème d'existence de takagi

Théorème d'existence de takagi

Théorème d'existence de Takagi

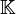En mathématiques et dans la théorie des corps de classes, le théorème d'existence de Takagi établit en partie que si \mathbb{K} est un corps de nombres avec un groupe de classes G, il existe une unique extension abélienne L/K avec un groupe de Galois G, tel que chaque idéal dans \mathbb{K}\, devient principal dans L, et que L est caractérisé par la propriété que c'est l'extension abélienne non ramifiée de 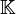\mathbb{K}\,. Le théorème nous dit que le corps de classes de Hilbert conjecturé par Hilbert existe toujours, mais il a été exigé par Artin et Furtwängler pour démontrer que cette principalisation apparaît.

Plus généralement, le théorème d'existence nous dit qu'il existe une correspondance d'inclusions bijectives entre les extensions abéliennes de 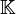\mathbb{K}\, et les groupes d'idéaux définis via des modules de 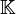\mathbb{K}\,. Ici, un module (ou diviseur de rayon) est un produit formel des valuations (aussi appelé premiers ou places) sur 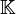\mathbb{K}\, vers les exposants entiers positifs. Les valuations archimédiennes incluent seulement ceux dont les compléments sont des nombres réels; ils peuvent être identifiés avec les ordres sur 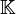\mathbb{K}\, et apparaîssent seulement avec un exposant un.

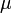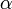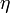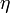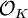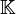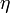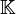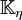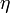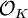Le module \mu\, est un produit de parties archimédiennes \alpha\, et de parties non-archimédiennes \eta\, et \eta\, peut être identifié avec un idéal dans l'anneau des entiers \mathcal{O}_K\, de \mathbb{K}\,. Le nombre de groupe mod \eta\, de \mathbb{K}\,, \mathbb{K}_\eta\,, est le groupe multiplicative des fractions u/v avec u différent de zéro et v premier vers \eta\, dans \mathcal{O}_K\,. 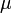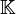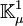Le rayon ou unité de rayon du groupe de nombre mod \mu\, de \mathbb{K}\,, \mathbb{K}_{\mu}^1\,, en plus des conditions sur u et v que 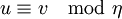u \equiv v \mod \eta\, et u/v > 0 dans chacun des ordres d'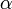\alpha\,. 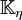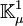Un groupe de nombre de rayon est maintenant un groupe se trouvant entre \mathbb{K}_\eta\, et \mathbb{K}_{\mu}^1\, et les groupes d'idéaux mod 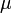\mu\, sont les idéaux fractionnaires premiers vers 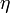\eta\, modulo un tel groupe de nombres de rayon. Ce sont ces groupes d'idéaux qui correspondent aux extensions abéliennes par le théorème d'existence.

Le théorème est dû à Teiji Takagi, qui le démontra pendant les années d'isolement de la Première Guerre mondiale et le présenta à la Conférence Internationale des Mathématiciens en 1920, conduisant au développement de la théorie classique de la théorie des corps de classes durant les années 1920. À la demande de Hilbert, l'article fut publié dans Mathematische Annalen en 1925.

Voir aussi

Formation de classes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me d%27existence de Takagi ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème d'existence de takagi de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Theoreme d'existence de Takagi — Théorème d existence de Takagi En mathématiques et dans la théorie des corps de classes, le théorème d existence de Takagi établit en partie que si est un corps de nombres avec un groupe de classes G, il existe une unique extension abélienne L/K… …   Wikipédia en Français

  • Théorème d'existence de Takagi — En mathématiques et dans la théorie des corps de classes, le théorème d existence de Takagi établit en partie que si K est un corps de nombres de groupe de classes G, il existe une unique extension abélienne L/K de groupe de Galois G telle que… …   Wikipédia en Français

  • Teiji Takagi — (高木 貞治 Takagi Teiji) né le 21 avril 1875 près de Gifu et mort le 28 février 1960 à Tokyo, était un mathématicien japonais, connu pour avoir prouvé le théorème d existence de Takagi en théorie des corps de classes. Il est né dans la région… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

  • Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”