- Théorie du portefeuille
-
Théorie moderne du portefeuille
La théorie moderne du portefeuille est une théorie financière développée en 1952 par Harry Markowitz. Elle expose comment des investisseurs rationnels utilisent la diversification afin d'optimiser leur portefeuille, et quel devrait être le prix d'un actif étant donné son risque par rapport au risque moyen du marché. Cette théorie fait appel aux concepts de frontière efficiente, coefficient bêta, droite de marché des capitaux et droite de marché des titres. Sa formalisation la plus accomplie est le modèle d'évaluation des actifs financiers ou MEDAF.
Dans ce modèle, le rendement d'un actif est une variable aléatoire et un portefeuille est une combinaison linéaire pondérée d'actifs. Par conséquent, le rendement d'un portefeuille est également une variable aléatoire et possède une espérance et une variance.
Sommaire
Idée de départ
L'idée de Markowitz dans sa gestion de portefeuille est simplement de panacher celui-ci d'une façon telle qu'on n'y fait pas de choix incohérents, conduisant par exemple à panacher des actions A et des actions B pour obtenir un couple revenu/risque moins bon à coût égal que ce qu'auraient procuré par exemple des actions C.
Sur le plan technique, il s'agit d'un problème d'optimisation quadratique assez banal. Son originalité est essentiellement l'application de ce modèle d'ingénieur au monde de la finance.
Hypothèses d'information, risque et rendement
Le modèle fait la double hypothèse que
- les marchés d'actifs financiers sont efficients. C'est l'hypothèse d'efficience du marché selon laquelle les prix et rendements des actifs sont censés refléter, de façon objective, toutes les informations disponibles concernant ces actifs.
- les investisseurs sont averses au risque (comme montré par Daniel Bernoulli) : ils ne seront prêts à prendre plus de risques qu'en échange d'un rendement plus élevé. À l'inverse, un investisseur qui souhaite améliorer la rentabilité de son portefeuille doit accepter de prendre plus de risques. L'équilibre risque/rendement jugé optimal dépend de la tolérance au risque de chaque investisseur.
Espérance et variance
On suppose généralement que la préférence de l'investisseur pour un couple risque / rendement peut être décrite par une fonction d'utilité quadratique. De plus, les évolutions du marché sont supposés suivre une distribution symétrique de Pareto. Par conséquent, seuls le rendement attendu (l'espérance de gain) et la volatilité (l'écart type) sont les paramètres examinés par l'investisseur. Ce dernier ne tient pas compte des autres caractéristiques de la distribution des gains, comme son asymétrie ou même le niveau de fortune investi.
Selon le modèle :
- le rendement d'un portefeuille est une combinaison linéaire de celui des actifs qui le composent, pondérés par leur poids wi dans le portefeuille. ;
- la volatilité du portefeuille est une fonction de la corrélation entre les actifs qui le composent. Cette fonction n'est pas linéaire.
Mathématiquement :
En général, pour un portefeuille comportant n actifs :
- Rendement attendu (espérance) :
- Variance du portefeuille :
- La variance du portefeuille est la somme des produits des poids wi de chaque couple d'actifs par leur covariance
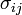 - cette somme inclut les poids au carré et les variances
- cette somme inclut les poids au carré et les variances 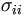 (ou
(ou 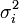 ) pour chaque actif i. La covariance est souvent exprimée en termes de corrélation
) pour chaque actif i. La covariance est souvent exprimée en termes de corrélation 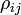 des rendements entre deux actifs où
des rendements entre deux actifs où 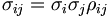
- Volatilité du portefeuille :
Cas particuliers :Pour un portefeuille composé de deux actifs :
- Espérance :
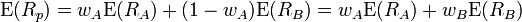
- Variance :
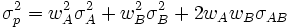
Lorsque le portefeuille est composé de trois actifs, la variance devient :
(Comme on le voit, plus le nombre n d'actifs grandit, plus la puissance de calcul nécessaire est importante : le nombre de termes de covariance est égal à n * (n-1) / 2. Pour cette raison, on utilise généralement des logiciels spécialisés. On peut néanmoins développer un modèle en utilisant des matrices ou dans une feuille de calcul d'un tableur.)Diversification
Un investisseur peut réduire le risque de son portefeuille simplement en détenant des actifs qui ne soient pas ou peu positivement corrélés, donc en diversifiant ses placements. Cela permet d'obtenir la même espérance de rendement en diminuant la volatilité du portefeuille.
Mathématiquement :
D'après les formules développées ci-avant, on comprend que lorsque le coefficient de corrélation entre deux actifs est inférieur à 0, la variance est plus petite que la simple somme pondérée des variances individuelles.
La frontière efficiente
Chaque couple possible d'actifs peut être représenté dans un graphique risque/rendement. Pour chaque rendement, il existe un portefeuille qui minimise le risque. À l'inverse, pour chaque niveau de risque, on peut trouver un portefeuille maximisant le rendement attendu. L'ensemble de ces portefeuilles est appelé frontière efficiente ou frontière de Markowitz.
Cette frontière est croissante par construction.
La région au-dessus de la frontière ne peut être atteinte en détenant seulement des actifs risqués. Un tel portefeuille est impossible à construire. Les points sous la frontière sont dits sous-optimaux, et n'intéresseront pas un investisseur rationnel.
L'actif sans risque
L'actif sans risque est un actif théorique qui rapporte le taux d'intérêt sans risque. Il est en général associé aux emprunts d'État à court terme. Cet actif possède une variance nulle, son rendement est donc connu à l'avance. Il n'est pas corrélé avec les autres actifs. Par conséquent, associé à un autre actif, il modifie linéairement l'espérance de rendement et la variance.
Le portefeuille devient donc :
- Espérance :
![\operatorname{E}(R_p) = (1 -w_A) \operatorname{E}(R_f) + w_A \operatorname{E}(R_A) = {E}(R_f) + w_A \operatorname[{E}(R_A) - {E}(R_f)]](/pictures/frwiki/97/a8806a2fc2a18ba1b01faa91dc3e891e.png)
- Soit encore :
![\operatorname{E}(R_p) = R_f + w_A \operatorname[{E}(R_A) - R_f]](/pictures/frwiki/102/f7108ac2eb3b54eaee0008521c5e43a4.png)
En conséquence, l'espérance de rentabilité est constituée de l'actif sans risque augmenté d'une prime de risque. En pratique, il convient de l'incorporer aux matrices S* et K* pour résoudre le lagrangien et ainsi déterminer le vecteur W*. C'est tout l'objet du développement de J. Tobin inscrit dans le prolongement des travaux de H. Markowitz.
'Porfolio leverage'
Portefeuille de marché
On comprend, d'après ce qui précède, que l'investisseur averti, cherchera la plus grande diversification possible jusqu'à atteindre cette limite appelée frontière efficiente. Elle se présente sous la forme d'une partie d'hyperbole (resp. de parabole) suivant que l'on soit dans un repère (écart-type, espérance de rendement) (resp. (variance, espérance de rendement)). Sachant maintenant que tous les investisseurs n'ont pas la même aversion au risque, certains choisiront de limiter leur risque en combinant par exemple une part d'actifs risqués complétée par l'actif sans risque. Pour déterminer ces types de portefeuilles "hybrides", on trace la courbe passant par l'actif sans risque et tangente à la frontière efficiente. Ce dernier point de contact constitue le portefeuille du marché. Les combinaisons de portefeuille sur le segment entre l'actif sans risque et le portefeuille du marché, dominent tous les autres portefeuilles.
Droite de marché des capitaux
Le choix du portefeuille par individu, par investisseur se fait sur la droite (RfM). Cette droite est la droite du marché des capitaux ou CML (capital market line). Normalement, chaque point représente un portefeuille. Son intérêt est qu'elle permet de visualiser l'ensemble des portefeuilles efficients disponibles qui regroupent simultanément des actifs risqués et des actifs sans risque. La proportion de l'un et de l'autre dépend de l'aversion au risque de l'investisseur. Caractéristiques de la droite de marché des capitaux : _ Le point d'intersection entre la droite et l'axe des ordonnées est le taux d'intérêt. Ce taux est le prix de renonciation à la consommation (à ce coût là, on refuse de consommer pour consommer plus demain)= le prix du temps. C'est le prix à payer à un agent pour qu'il accepte de différer sa consommation dans le temps. _ Le point de tangence indique le compromis entre le taux de rentabilité et le risque. C'est le prix du risque. On accepte un risque plus grand si on a une rentabilité plus élevée.
Évaluation des actifs
Risque systématique et risque spécifique
Modèle d'évaluation des actifs financiers (CAPM)
On suppose que les marchés financiers sont parfaits au sens des hypothèses de la concurrence. Il n'y a pas d'impôt, pas de barrières à l'entrée et une absence de coût de transaction. L'information est disponible gratuitement pour tous les agents. Les agents sont des preneurs de prix et ils ont tous intérêt à combiner deux actifs.
Selon ce modèle, le rendement exigé sur un actif est fonction de son risque systématique. Plus précisément, on a:
Une fois ce rendement obtenu, on obtient la valeur de l'actif en actualisant ses flux avec comme taux le rendement exigé.
Droite de marché des titres (SML)
Voir aussi
Bibliographie
- Harry Markowitz. (1952). Portfolio Selection, Journal of Finance, 7 (1), 77-91.
- William Forsyth Sharpe (1964). Capital asset prices: A theory of market equilibrium under conditions of risk, Journal of Finance, 19(3), 425-442.
- Lintner, J. (1965). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets, Review of Economics and Statistics, 47
- Tobin, James (1958). Liquidity preference as behavior towards risk, The Review of Economic Studies, 25, 65-86.
- La Théorie moderne du portefeuille, Florin Aftalion, Patrice Poncet, Que sais je?, ISBN 2130497683
- Portail de la finance
- Portail de l’économie
Catégories : Finance de marché | Gestion d'actifs | Thèmes généraux de finance | Management | Risque (finance) | Système bancaire
Wikimedia Foundation. 2010.

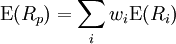
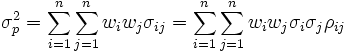
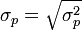
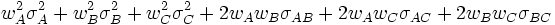
![E(R_{actif}) = R_F + \beta_{actif}\cdot [E(R_M) - R_F]](/pictures/frwiki/99/cc575bba3d4b39504da4dc545d6440cc.png)