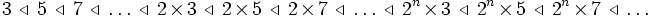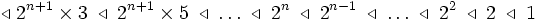Theoreme de Sarkovskii

Theoreme de Sarkovskii

Théorème de Sarkovskii

Le théorème de Sarkovskii est un théorème de mathématiques portant sur l'itération des fonctions continues. Il donne des contraintes sur la présence de points périodiques lorsqu'on itère la fonction f, c'est-à-dire de points x0 tels que la suite xn+1=f(xn) correspondante soit périodique.

Ce théorème fait partie des premiers exemples remarquables de la théorie des systèmes dynamiques, introduisant la notion de chaos. Sa popularité est telle qu'il se retient souvent sous la forme d'un « slogan », correspondant à un énoncé simplifié :

3-cycle implique chaos

Il faut comprendre par là que toute fonction continue présentant un cycle de période 3 admet un cycle de période n pour tout entier n.

Forme générale du théorème

Avant de l'exposer, nous devons d'abord définir l'ordre de Sarkovskii.

L'ordre de Sarkovskii est une relation d'ordre définie sur les entiers strictement positifs de la façon suivante :

3 \;\triangleleft\; 5 \;\triangleleft\; 7 \;\triangleleft\; \ldots \;\triangleleft\; 2\times 3 \;\triangleleft\; 2\times 5 \;\triangleleft\; 2\times 7 \;\triangleleft\; \ldots \;\triangleleft\; 2^n\times 3 \;\triangleleft\; 2^n\times 5 \;\triangleleft\; 2^n\times 7 \;\triangleleft\; \ldots
\;\triangleleft\; 2^{n+1}\times 3 \;\triangleleft\; 2^{n+1}\times 5 \;\triangleleft\; \ldots \;\triangleleft\; 2^n \;\triangleleft\; 2^{n-1} \;\triangleleft\; \ldots \;\triangleleft\; 2^2 \;\triangleleft\; 2 \;\triangleleft\; 1

Autrement dit, on place d'abord les impairs à partir de 3 par ordre croissant, puis les impairs multipliés par 2, puis par 4, etc. et on termine par les puissances de 2 par ordre décroissant.

Le théorème de Sarkovskii s'énonce alors comme suit :

Soit f une fonction continue sur un intervalle I, à valeurs dans I. Si f admet un point périodique de période n, alors pour tout m succédant à n dans l'ordre de Sarkovskii, f admet un point périodique de période m .


x est un point périodique de période n si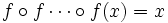 f \circ f \cdots \circ f(x) = x où f apparaît n fois, et où n est le plus petit entier vérifiant cette propriété. Ainsi, si f admet un point périodique de période 3, alors f admet des points périodiques de n'importe quelle période.

Voir aussi

Références

  • A. N. Sharkovsky, Coexistence of cycles of a continuous map of a line into itself, Internat. J. Chaos Appl. Sci. Engrg. 5 (1995) 1263-1273, traduction anglaise de l'article initial paru en russe dans Ukrain. Math. Zh. 16 (1964) 61-71.
  • T. Li & J. Yorke, Period three implies chaos, Amer. Math. Monthly, 82 (1975) 985-992
  • B.S. Du, A simple proof of Sharkovsky's theorem, Amer. Math. Monthly 111 (2004) 595-599.
  • B.S. Du, A simple proof of Sharkovsky's theorem revisited, Amer. Math. Monthly 114 (2007) 152-155.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Sarkovskii ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Sarkovskii de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Théorème de Sarkovskii — Le théorème de Sarkovskii est un théorème de mathématiques portant sur l itération des fonctions continues. Il donne des contraintes sur la présence de points périodiques lorsqu on itère la fonction f, c est à dire de points x0 tels que la suite… …   Wikipédia en Français

  • Théorème de sarkovskii — Le théorème de Sarkovskii est un théorème de mathématiques portant sur l itération des fonctions continues. Il donne des contraintes sur la présence de points périodiques lorsqu on itère la fonction f, c est à dire de points x0 tels que la suite… …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

  • Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Systeme dynamique — Système dynamique Pour consulter un article plus général, voir : Systèmes dynamiques. En mathématiques, en physique théorique et en ingénierie, un système dynamique est un système classique[1] qui évolue au cours du temps de façon à la… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”