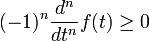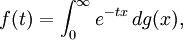Theoreme de Bernstein

Theoreme de Bernstein

Théorème de Bernstein

En analyse fonctionnelle, une branche des mathématiques, le théorème de Bernstein établit que toute fonction à valeurs réelles sur la demi-droite [0, ∞) qui est totalement monotone est une combinaison (dans un cas important, une moyenne pondérée ou une espérance mathématique) d'exponentielles.

La monotonie totale (on dit aussi complète) d'une fonction f signifie que la relation :

(-1)^n{d^n \over dt^n} f(t) \geq 0

est vérifée pour tous les entiers naturels n et tous les réels t ≥ 0. La moyenne pondérée peut alors être caractérisée : il existe une mesure de Borel positive ou nulle sur [0, ∞), avec une fonction de distribution cumulative g telle que :

f(t) = \int_0^\infty e^{-tx} \,dg(x),

l'intégrale étant une intégrale selon Riemann-Stieltjes.

Dans un langage plus abstrait, le théorème caractérise les transformées de Laplace des mesures de Borel positives sur [0,∞). Sous cette forme, il est connu sous le nom de théorème de Bernstein-Widder, ou de Hausdorff-Bernstein-Widder. Hausdorff avait déjà caractérisé les séquences complètement monotones.

Références

  • S. N. Bernstein, Sur les fonctions absolument monotones, Acta Mathematica 1928 pp.1-66 ;
  • D. Widder (1941) The Laplace Transform.

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Bernstein ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Bernstein de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Théorème de bernstein — En analyse fonctionnelle, une branche des mathématiques, le théorème de Bernstein établit que toute fonction à valeurs réelles sur la demi droite [0, ∞) qui est totalement monotone est une combinaison (dans un cas important, une moyenne… …   Wikipédia en Français

  • Théorème de Bernstein — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Plusieurs théorèmes sont dus à divers mathématiciens portant le nom de Bernstein  . Sergeï Natanovitch Bernstein : théorème de Bernstein sur les …   Wikipédia en Français

  • Théorème de Bernstein sur les fonctions monotones — Pour les articles homonymes, voir Théorème de Bernstein. En analyse fonctionnelle, une branche des mathématiques, le théorème de Bernstein, établit que toute fonction à valeurs réelles sur la demi droite [0, ∞) qui est totalement monotone… …   Wikipédia en Français

  • Théorème de Cantor-Bernstein — Pour les articles homonymes, voir Théorème de Bernstein. Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg… …   Wikipédia en Français

  • Bernstein — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Patronyme 2 Toponymes 3 Lieux …   Wikipédia en Français

  • Theoreme de Cantor-Bernstein — Théorème de Cantor Bernstein Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst …   Wikipédia en Français

  • Théorème de Cantor-Schröder-Bernstein — Théorème de Cantor Bernstein Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst …   Wikipédia en Français

  • Théorème de Schröder-Bernstein — Théorème de Cantor Bernstein Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst …   Wikipédia en Français

  • Théorème de cantor-bernstein — Le théorème de Cantor Bernstein, également appelé théorème de Cantor Schröder Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst Schröder. Cantor en donna… …   Wikipédia en Français

  • Theoreme de Stone-Weierstrass — Théorème de Stone Weierstrass Le théorème d approximation de Weierstrass affirme que toute fonction continue définie sur un compact peut être approchée aussi près que l on veut par une fonction polynomiale. Parce que les fonctions polynômes sont… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”