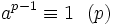Test de primalité de fermat

Test de primalité de Fermat

Le petit théorème de Fermat affirme que si p est un nombre premier et si a est premier avec p, alors a^p-1 - 1 est divisible par p. Ceci peut être aussi écrit

$a^{p-1}\equiv 1 \ \ (p)$

(pour mod voir arithmétique modulaire)

La réciproque de ce théorème est fausse, par exemple : 561=3×11×17 n'est pas premier et pourtant pour tout entier a premier avec 561, on a 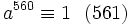$a^{560}\equiv 1 \ \ (561)$ (voir les nombres de Carmichaël)

Mais nous pouvons tout de même écrire :

Si p est composé, alors $a p - 1$ est de façon improbable, congru à 1 modulo p pour une valeur arbitraire de a

ce qui représente une sorte de réciproque probabiliste du théorème.

Le logiciel de chiffrement PGP tire profit de cette propriété du théorème pour examiner si les grands nombres aléatoires qu'il choisit sont premiers. Il examine les valeurs que nous appellerons x en utilisant quatre valeurs de a (appelées témoins) en employant la formule ci-dessus. Ces quatre valeurs sont 2, 3, 5 et 7, les quatre premiers nombres premiers.

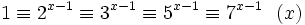$1\equiv 2^{x-1}\equiv 3^{x-1}\equiv 5^{x-1}\equiv 7^{x-1} \ \ (x)$ , alors nous savons que le nombre x est probablement premier.

Si l'une quelconque de ces équations donne une valeur autre que 1, alors x est définitivement composé. Utiliser des témoins supplémentaires diminue la chance qu'un nombre composé x soit considéré premier, bien que très peu de grands nombres puissent duper les 4 témoins.

L'article sur les nombres pseudopremiers donne une explication détaillée sur les nombres qui dupent les tests de primalité de ce type.

Portail des mathématiques

Ce document provient de « Test de primalit%C3%A9 de Fermat ».

Catégorie : Test de primalité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Test de primalité de fermat de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Test de primalite de Fermat — Test de primalité de Fermat Le petit théorème de Fermat affirme que si p est un nombre premier et si a est premier avec p, alors ap 1 1 est divisible par p. Ceci peut être aussi écrit (pour mod voir arithmétique modulaire) La réciproque de ce… … Wikipédia en Français
Test de primalité de Fermat — Le petit théorème de Fermat affirme que si p est un nombre premier et si a est premier avec p, alors ap 1 1 est divisible par p. Ceci peut être aussi écrit (pour mod voir arithmétique modulaire) La réciproque de ce théorème est fausse, par… … Wikipédia en Français
Test de primalite de Miller-Rabin — Test de primalité de Miller Rabin Le test de primalité de Miller Rabin est un test de primalité probabiliste : c’est à dire un algorithme qui détermine si un nombre donné est probablement premier, de façon similaire au test de primalité de… … Wikipédia en Français
Test de primalité de miller-rabin — Le test de primalité de Miller Rabin est un test de primalité probabiliste : c’est à dire un algorithme qui détermine si un nombre donné est probablement premier, de façon similaire au test de primalité de Fermat et le test de primalité de… … Wikipédia en Français
Test de primalite de Solovay-Strassen — Test de primalité de Solovay Strassen Le test de primalité de Solovay Strassen, dû à Robert M. Solovay et Volker Strassen, est un test probabiliste permettant de déterminer si un nombre impair est un nombre composé ou un nombre premier probable.… … Wikipédia en Français
Test de primalité de solovay-strassen — Le test de primalité de Solovay Strassen, dû à Robert M. Solovay et Volker Strassen, est un test probabiliste permettant de déterminer si un nombre impair est un nombre composé ou un nombre premier probable. Les concepts Le mathématicien suisse… … Wikipédia en Français
Test de primalite — Test de primalité Un test de primalité est un algorithme permettant de savoir si un nombre entier est premier. Sommaire 1 Méthode naïve 2 Tests probabilistes 3 Tests déterministes rapides … Wikipédia en Français
Test de primalite AKS — Test de primalité AKS Le test de primalité AKS (aussi connu comme le test de primalité Agrawal Kayal Saxena et le test cyclotomique AKS) est un algorithme déterministe de preuve de primalité découvert et publié le 6 août 2002 par trois… … Wikipédia en Français
Test de primalité aks — Le test de primalité AKS (aussi connu comme le test de primalité Agrawal Kayal Saxena et le test cyclotomique AKS) est un algorithme déterministe de preuve de primalité découvert et publié le 6 août 2002 par trois scientifiques indiens nommés… … Wikipédia en Français
Test de primalité de Miller-Rabin — Le test de primalité de Miller Rabin est un test de primalité probabiliste : c’est à dire un algorithme qui détermine si un nombre donné est probablement premier, de façon similaire au test de primalité de Fermat et le test de primalité de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Test de primalité de fermat