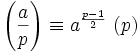Test de primalité de solovay-strassen

Test de primalité de Solovay-Strassen

Le test de primalité de Solovay-Strassen, dû à Robert M. Solovay et Volker Strassen, est un test probabiliste permettant de déterminer si un nombre impair est un nombre composé ou un nombre premier probable.

Les concepts

Le mathématicien suisse Euler a démontré que pour tout nombre premier p impair,

$\left(\frac{a}{p}\right) \equiv a^{p-1 \over 2}\ (p)$

où

$\left(\frac{a}{p}\right)$

est le symbole de Legendre.

Ainsi, pour déterminer si un entier impair p donné est premier, nous pouvons nous assurer que pour un grand nombre de valeurs aléatoires de a, l’égalité est bien vérifiée. Si elle est fausse pour un certain entier a, alors nous savons que p n’est pas premier.

Cependant, tout comme avec le test de primalité de Fermat, il y a des menteurs. Une valeur a est appelée menteur d’Euler si l’égalité est vérifiée bien que p soit composé. Un témoin d’Euler est une valeur de a pour laquelle l’égalité n'est pas vérifiée, et donc a est un témoin du fait que p est composé.

À la différence du test de primalité de Fermat, pour chaque entier composé p au moins la moitié de tous les a de 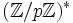$(\mathbb{Z}/p\mathbb{Z})^*$ sont des témoins d’Euler. Par conséquent, il n’y a aucune valeur de p pour laquelle tous les a sont des menteurs, comme les nombres de Carmichael pour le test de Fermat.

Algorithme et performance

L’algorithme peut être écrit comme suit :

Entrées : n : variable entière impaire dont on veut connaître la primalité ; k : variable qui représente le nombre de fois où la primalité va être testée.

Sortie : composé si n est composé, sinon probablement premier

répéter k fois :

choisir a au hasard entre 1 et n-1

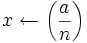
$x\leftarrow \left(\frac{a}{n}\right)$

si x = 0 ou 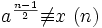$a^{\frac{n-1}{2}}\not\equiv x\ (n)$ alors retourne composé

retourne probablement premier

En utilisant des algorithmes rapides d’exponentiation modulaire, la performance de cet algorithme est un O(k × log³p), où k est le nombre de fois où nous essayons aléatoirement un entier a, et p est la valeur dont nous voulons examiner la primalité. La probabilité pour que l’algorithme échoue est inférieure à 2^{- k}.

Dans les applications en cryptographie, si nous choisissons une valeur suffisamment grande de k, comme par exemple 100, la probabilité pour que l’algorithme échoue est si petite que nous pouvons employer le nombre premier dans des applications cryptographiques sans inquiétude.

Portail des mathématiques

Ce document provient de « Test de primalit%C3%A9 de Solovay-Strassen ».

Catégorie : Test de primalité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Test de primalité de solovay-strassen de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Test de primalite de Solovay-Strassen — Test de primalité de Solovay Strassen Le test de primalité de Solovay Strassen, dû à Robert M. Solovay et Volker Strassen, est un test probabiliste permettant de déterminer si un nombre impair est un nombre composé ou un nombre premier probable.… … Wikipédia en Français
Test de primalité de Solovay-Strassen — Le test de primalité de Solovay Strassen, dû à Robert M. Solovay et Volker Strassen, est un test probabiliste permettant de déterminer si un nombre impair est un nombre composé ou un nombre premier probable. Les concepts Le mathématicien suisse… … Wikipédia en Français
Test de primalite de Miller-Rabin — Test de primalité de Miller Rabin Le test de primalité de Miller Rabin est un test de primalité probabiliste : c’est à dire un algorithme qui détermine si un nombre donné est probablement premier, de façon similaire au test de primalité de… … Wikipédia en Français
Test de primalité de miller-rabin — Le test de primalité de Miller Rabin est un test de primalité probabiliste : c’est à dire un algorithme qui détermine si un nombre donné est probablement premier, de façon similaire au test de primalité de Fermat et le test de primalité de… … Wikipédia en Français
Test de primalite — Test de primalité Un test de primalité est un algorithme permettant de savoir si un nombre entier est premier. Sommaire 1 Méthode naïve 2 Tests probabilistes 3 Tests déterministes rapides … Wikipédia en Français
Test de primalite AKS — Test de primalité AKS Le test de primalité AKS (aussi connu comme le test de primalité Agrawal Kayal Saxena et le test cyclotomique AKS) est un algorithme déterministe de preuve de primalité découvert et publié le 6 août 2002 par trois… … Wikipédia en Français
Test de primalité aks — Le test de primalité AKS (aussi connu comme le test de primalité Agrawal Kayal Saxena et le test cyclotomique AKS) est un algorithme déterministe de preuve de primalité découvert et publié le 6 août 2002 par trois scientifiques indiens nommés… … Wikipédia en Français
Test de primalité de Miller-Rabin — Le test de primalité de Miller Rabin est un test de primalité probabiliste : c’est à dire un algorithme qui détermine si un nombre donné est probablement premier, de façon similaire au test de primalité de Fermat et le test de primalité de… … Wikipédia en Français
Test de primalité AKS — Le test de primalité AKS (aussi connu comme le test de primalité Agrawal Kayal Saxena et le test cyclotomique AKS) est un algorithme déterministe de preuve de primalité découvert et publié le 6 août 2002 par trois scientifiques indiens nommés… … Wikipédia en Français
Test de primalité — Un test de primalité est un algorithme permettant de savoir si un nombre entier est premier. Sommaire 1 Méthode naïve 2 Tests probabilistes 3 Tests déterministes rapides … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Test de primalité de solovay-strassen