Systèmes dynamiques

Les systèmes dynamiques désignent couramment la branche de recherche active des mathématiques, à la frontière de la topologie, de l'analyse, de la géométrie, de la théorie de la mesure et des probabilités, et qui s'efforce d'étudier les propriétés d'un système dynamique. La nature de cette étude diffère suivant le système dynamique étudié, nature qui dépend des outils utilisés (analytiques, géométriques ou probabilistes).

Historiquement, les premières questions relevant des systèmes dynamiques concernaient la mécanique à une époque où elle était incluse dans l'enseignement des mathématiques. Une des questions majeures et qui a motivé la recherche mathématique est le problème de la stabilité du système solaire. Les travaux de Lagrange sur le sujet consistèrent à interpréter l'influence des corps autres que le Soleil sur une planète comme une succession de chocs infinitésimaux : ces travaux retrouvent des échos dans le théorème KAM (Kolmogorov - Arnold - Moser).

Les systèmes dynamiques se sont développés et spécialisés au cours du XIX^e siècle. Ils concernaient en premier lieu l'itération des applications continues et la stabilité des équations différentielles. Mais progressivement, au fur et à mesure de la diversification des mathématiques, les systèmes dynamiques se sont considérablement élargis. Ils comprennent aujourd'hui l'étude des actions continues de groupes, dont l'intérêt réside dans ses applications en géométrie, et la théorie ergodique, née de l'avènement de la théorie de la mesure et qui trouve ses échos en probabilités.

Sommaire 1 La diversité d'étude 1.1 Équations différentielles 1.2 Itération d'applications continues 1.3 La théorie ergodique 1.4 L'étude des actions continues de groupes 2 L'unicité des systèmes dynamiques 2.1 Espace des phases 2.2 Comportement asymptotique 2.3 Stabilité 3 Culture populaire 3.1 La théorie du chaos 3.2 Les ensembles de Mandelbrot 4 Notes et références 5 Voir aussi

La diversité d'étude

Équations différentielles

L'étude du comportement des équations différentielles sont à l'origine des systèmes dynamiques. Les questions qui occurent sont de plusieurs natures. Elles concernent :

• le comportement limite des solutions ;
• la stabilité des solutions par rapport aux conditions initiales ;
• la stabilité des solutions par rapport à des perturbations portant sur l'équation différentielle.

Un cas relativement simple en apparence est l'étude des équations différentielles homogènes d'ordre 1. Ces équations différentielles se résument à la donnée d'un champ de vecteurs sur un ouvert d'un espace vectoriel réel, dont on cherche les courbes dites intégrales. L'étude des champs de vecteurs a un impact en géométrie différentielle.

Itération d'applications continues

L'itération consiste à considérer les composées successives fⁿ d'une certaine application continue f. Les puissances sont en général positives, mais peuvent être négatives lorsque l'inverse de f est défini. L'étude porte essentiellement sur ses propriétés limites.

L'intérêt porté à l'itération d'applications continues vint suite aux travaux de Poincaré sur la stabilité du Système Solaire. C'est à cette occasion qu'a été introduite l'application de premier retour de Poincaré. L'application de retour de Poincaré et son opération inverse connue sous le nom de suspension permet de passer d'un champ de vecteurs au problème de l'itération d'une application.

On distingue habituellement :

• Un système dynamique continu : la donnée d'un espace topologique séparé X et d'une application continue 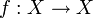, souvent un homéomorphisme ;
• Un système dynamique différentiable : la donnée d'une variété différentielle réelle X et d'une application différentiable 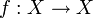, souvent un difféomorphisme (il est souvent d'usage d'imposer un degré de régularité) ;
• Un système dynamique complexe : la donnée d'une variété holomorphe X et d'une application holomorphe 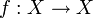, souvent un biholomorphisme.

Le cas échéant, on accole l'adjectif compact pour signaler que X est supposé compact. L'étude d'un système dynamique différentiable et de ses particularités s'appelle la dynamique différentiable et l'étude d'un système dynamique holomorphe la dynamique holomorphe.

Les homéomorphismes du cercle semblent à tort être un cas d'étude simple, mais montrent au contaire la complexité des questions qui se posent. La classification des C^1-difféomorphismes dont la dérivée est à variation bornée est déterminée par un invariant appelé le nombre de rotation. Une recherche actuelle tend à généraliser ces résultats en dimension supérieure.

La théorie ergodique

La théorie ergodique concerne l'étude des applications mesurables préservant une mesure donnée et de leur itération. Trouvant ses origines dans les interrogations du physicien Boltzmann en 1871, elle s'est constituée véritablement comme domaine de recherche mathématique dans le tournant du XXe siècle. L'introduction de la théorie de la mesure par Lebesgue a permis d'introduire un cadre d'étude et d'élargir le domaine de questions d'analyse à des questions probabilistes. L'un des premiers grands théorèmes est le théorème ergodique de Birkhoff : sous de bonnes hypothèses, la moyenne dite spatiale d'un flot est égale à la moyenne dite temporelle le long d'une orbite donnée.

La théorie ergodique trouve des applications notamment en physique statistique, domaine actif de la recherche physique née des travaux de Boltzman sur les gaz classiques cinétiques.

On a coutume de distinguer :

• Un système dynamique mesurable : la donnée d'un espace mesurable X et d'une application mesurable 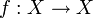, éventuellement admettant un inverse presque partout ;
• Un système dynamique mesuré : la donnée d'un espace mesuré X de mesure μ et d'une application mesurable 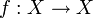préservant la mesure μ, éventuellement admettant un inverse presque partout qui préserve aussi la mesure μ ;
• Un système dynamique continu mesuré : la donnée d'un espace topologique X muni d'une mesure borélienne μ, et d'une application continue 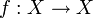préservant la mesure μ, éventuellement un homéomorphisme dont l'inverse préserve aussi la mesure μ.

L'étude des actions continues de groupes

Les actions continues d'un groupe topologique sur un espace topologique peuvent être vues comme une généralisation des flots continus. Dans ce langage, un flot continu est une action continue du groupe additif R.

Pour les groupes topologiques localement compacts, l'existence d'une mesure de Haar permet d'inclure des méthodes de la théorie de la mesure. En particulier ont été formalisées des notions de moyennabilité.

En géométrie différentielle, l'intérêt porte sur l'étude des actions différentiables des groupes de Lie sur les variétés différentielles.

L'unicité des systèmes dynamiques

Malgré la diversification de son champ d'action, ce domaine mathématique garde une unité tant dans les questions posées que dans la description des objets étudiés.

Espace des phases

Quelle que soit sa nature (topologique, différentiable, mesurable, mesuré, ...), un système dynamique est la donnée conjointe :

• D'un espace des phases,
• D'un temps, qui peut être discret (entiers naturels, entiers relatifs, groupe discret), continu (réels positifs, réels, groupe de Lie connexe), ...
• D'une loi d'évolution.

Comportement asymptotique

Stabilité

Culture populaire

Un certain nombre de résultats des systèmes dynamiques ont eu un impact non négligeables dans la culture populaire. En particulier, la théorie du chaos pour les systèmes dynamiques continus et les ensembles de Mandelbrot en dynamique holomorphe ont eu un impact dans les domaines artistiques.

La théorie du chaos

La théorie du chaos est un ensemble de méthodes mathématiques apparaissant et dans les itérations d'applications continues et dans les questions de stabilité des équations différentielles, qui tend à mettre en valeur une sensibilité en la ou en les conditions initiales.

La suite logistique et le chat d'Arnold figurent parmi les exemples classiques relevant de la théorie du chaos. Cependant, l'exemple des systèmes dynamiques hyperboliques est plus représentatif des phénomènes chaotiques. Un modèle simple mais déjà présentant une dynamique assez riche est celui des difféomorphismes hyperboliques du tore (en toute dimension).

Les systèmes chaotiques présentent en général une très grande stabilité structurelle. Dit informellement, une perturbation portant non plus sur des conditions initiales mais sur la loi de transformation ne modifie pas en général la dynamique globale. C'est le cas par exemple des systèmes dynamiques hyperboliques.

Un outil central pour prouver qu'un système dynamique est chaotique est de faire usage des méthodes dites de codage ou de partitions de Markov.

Dans la culture populaire, la théorie du chaos se dit de toute structure sociale ou phénomène social dont on ne maitrise pas les causes ou le développement.

Dans les romans Jurassic Park et Le Monde perdu de Michael Crichton, c'est ce point de vue populaire qui est présenté par le mathématicien fictif Ian Malcolm.

Les ensembles de Mandelbrot

Notes et références

• John Hubbard et Berly West, Differential equations : a dynamical system approach.
• Robert L. Devaney, Introduction to Chaotic Dynamical Systems

Voir aussi

• Système dynamique (article doublon)

• Portail des mathématiques