- Symétrie axiale
-
Une symétrie d'axe p.
La symétrie axiale ou réflexion est une transformation géométrique du plan qui modélise un "pliage" ou un "effet miroir".
La symétrie axiale, d'axe la droite d, laisse tous les points de d invariants et transforme tout point M, non situé sur d, en un point image M' tel que :
- La droite (MM' ) soit perpendiculaire à l'axe de symétrie d.
- Le milieu du segment [MM' ] appartient à l'axe de symétrie d.
Le point M' est alors appelé le symétrique de M par rapport à l'axe de symétrie d.
Dans le cas d'une figure plane globalement invariante par une symétrie d'axe d, la droite d est dite axe de symétrie de la figure.
La symétrie axiale est un cas particulier de symétrie. Elle est une involution, c'est-à-dire qu'on retrouve le point ou la figure de départ si on l'applique deux fois.
Sommaire
Propriétés de la symétrie axiale
Propriété de superposition
Deux figures sont symétriques par rapport à un axe d lorsqu' elles se superposent après pliage le long de la droite d.
Propriété de conservation
La symétrie axiale est une isométrie, elle conserve:
- Les distances
- Les parallèles (les symétriques de deux droites parallèles sont parallèles)
- Les angles géométriques (le symétrique d'un angle est un angle de même mesure) mais ne conserve pas les angles orientés.
- Les périmètres (le symétrique d'une figure est une figure de même périmètre)
- Les aires (le symétrique d'une figure est une figure de même aire)
Exemples
- Si M appartient à la droite d alors M' = M.
On notera que le symétrique d'une droite est une droite pour les exemples suivants:
- Si une droite est sécante à l'axe de symétrie d en M, il en sera de même pour son symétrique.
- Si une droite est parallèle à l'axe de symétrie d, il en sera de même pour son symétrique.
- Si une droite est perpendiculaire à l'axe de symétrie d, elle est son propre symétrique.
- Le symétrique d'un cercle C, ayant pour centre O et pour rayon r, par rapport à une droite d est un cercle C' , ayant pour centre O' le symétrique de O par rapport à d et pour même rayon r.
La construction du symétrique d'un point M par rapport à une droite d
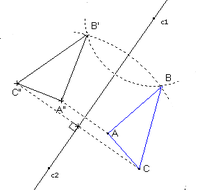Un triangle (ABC) et son image (A'B'C') par la symétrie d'axe (c1c2). Le point B' est construit au compas seul tandis que C' est construit avec l'équerre.A la règle graduée et à l'équerre
- Tracer la droite d.
- Placer le point M distinct de la droite d.
- Tracer la droite passant par M et perpendiculaire à la droite d et noter I le point d'intersection des deux droites.
- Placer sur la droite (MI) le point M' symétrique de M par rapport à la droite d tel que MI = IM' .
Au compas seul
- Tracer la droite d.
- Placer le point M distinct de la droite d.
- Placer deux points distincts A et B sur la droite d.
- Tracer l'arc de cercle de centre A et de rayon AM.
- Tracer l'arc de cercle de centre B et de rayon BM.
- Les deux arcs de cercle se recoupent en un point M' symétrique de M par rapport à d.
Voir aussi
Wikimedia Foundation. 2010.
