Symétrie axiale (mathématiques élémentaires)

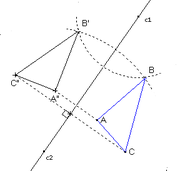
En mathématiques élémentaires, la symétrie axiale ou symétrie d'axe (d) est la transformation du plan, qui au point M associe son symétrique par rapport à la droite (d).

Le symétrique du point M par rapport à la droite (d) peut être obtenu par simple pliage de la feuille de papier suivant la droite (d) mais il existe aussi une définition mathématique de cette notion et des méthodes géométriques de construction à la règle et/ou au compas.

La symétrie axiale porte aussi le nom de symétrie orthogonale d'axe (d) ou de réflexion d'axe (d).

Sommaire 1 Définition 2 Constructions du symétrique d'un point par rapport à une droite 2.1 A la règle graduée et à l'équerre 2.2 Au compas seul 3 Propriétés 4 Voir aussi

Définition

Soit (d) une droite et M un point non situé sur (d).

On dit que le point M' est le symétrique de M par rapport à (d) si, et seulement si,(d) est la médiatrice de [ MM' ].

On dit alors que (d) est l' axe de symétrie du segment [ MM' ].

On convient de dire que tout point de (d) est son propre symétrique.

Constructions du symétrique d'un point par rapport à une droite

A la règle graduée et à l'équerre

• Tracer la droite passant par M et perpendiculaire à (d).
• Soit H le point d'intersection de cette droite et de (d).
• Placer sur (MH) le point M' tel que MH = HM' .

Alors, M' est le symétrique de M par rapport à (d).

Au compas seul

• Choisir deux points distincts A et B sur la droite (d).
• Tracer l'arc de cercle de centre A et de rayon AM.
• Tracer l'arc de cercle de centre B et de rayon BM.
• Ces deux arcs de cercle se recoupent en un point M' ,qui est le symétrique de M par rapport à (d).

Propriétés

NB : Ici,lorsque nous disons "symétrique", il faut comprendre symétrique par rapport à une droite.

• Deux figures sont symétriques pa rapport à (d) lorsqu' elles se superposent après pliage le long de la droite (d);
• Si le point M' est le symétrique du point M par rapport à (d) alors le point M est le symétrique du point M' par rapport à (d). On dit que la symétrie axiale est involutive;
• Le symétrique d'une droite est une droite. Si la première droite coupe l'axe (d) en M, la seconde coupera l'axe (d) au même point. Si l'une des droites est parallèle à l'axe de symétrie, il en est de même de la seconde. Si une droite est perpendiculaire à l'axe de symétrie, elle est son propre symétrique;
• Le symétrique d'un cercle C de centre O et de rayon r est un cercle C' de centre O' , le symétrique de O, et de même rayon r.
• Propriété "de conservation" : La symétrie axiale est une isométrie, elle conserve:
  • les longueurs;
  • les angles (le symétrique d'un angle est un angle de même mesure);

  et conserve donc également:

  • les parallèles (les symétriques de deux droites parallèles sont parallèles);
  • les aires (le symétrique d'une figure est une figure de même aire);
  • les périmètres (le symétrique d'une figure est une figure de même périmètre).

Mais elle ne conserve pas l'orientation : quand le point M tourne autour de O dans le sens des aiguilles d'une montre, son symétrique M' tourne autour de O' dans le sens inverse.

Voir aussi

• Symétrie centrale (mathématiques élémentaires);
• Symétrie (transformation géométrique).

• Portail de la géométrie