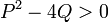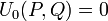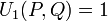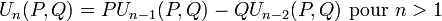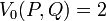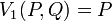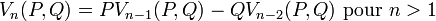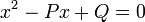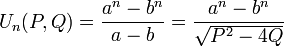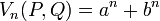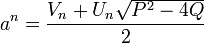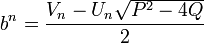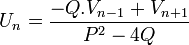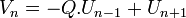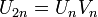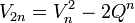Suite de lucas

Suite de lucas

Suite de Lucas

En mathématiques, une suite de Lucas est une généralisation de la suite de Fibonacci et des nombres de Lucas. Les suites de Lucas furent étudiées en premier par le mathématicien français Édouard Lucas.

Sommaire

Relations de récurrence

Soient deux entiers donnés P et Q qui satisfont

P^2 - 4Q > 0\,

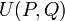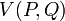les suites de Lucas U(P,Q)\, et V(P,Q)\, sont définies par les relations de récurrence linéaire

U_0(P,Q) = 0\,
U_1(P,Q) = 1\,
U_n(P,Q)=PU_{n-1}(P,Q)-QU_{n-2}(P,Q) \mbox{ pour }n>1\,

et

V_0(P,Q)=2\,
V_1(P,Q)=P\,
V_n(P,Q)=PV_{n-1}(P,Q)-QV_{n-2}(P,Q) \mbox{ pour }n>1\,

Terme général

Selon la méthode de calcul sur des suites à récurrence linéaire, il suffit de chercher les racines du polynôme caractéristique

x^2 - Px + Q = 0\,

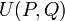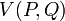Puisque P2 − 4Q > 0, ce polynôme possède deux racines qui sont a et b. Alors U(P,Q)\, et V(P,Q)\, peuvent aussi être définies en fonction de a et b par

U_n(P,Q)= \frac{a^n-b^n}{a-b} = \frac{a^n-b^n}{ \sqrt{P^2-4Q}}\,
V_n(P,Q)=a^n+b^n\,

à partir desquelles nous pouvons extraire les relations

a^n = \frac{V_n + U_n \sqrt{P^2-4Q}}{2}\,
b^n = \frac{V_n - U_n \sqrt{P^2-4Q}}{2}\,

Autres relations

Les nombres dans les suites de Lucas satisfont aux relations qui sont analogues à celles entre les nombres de Fibonacci et les nombres de Lucas. Par exemple :

U_n = \frac{-Q.V_{n-1} + V_{n+1}}{P^2-4Q}\,
V_n = -Q.U_{n-1} + U_{n+1}\,
U_{2n} = U_n V_n\,
V_{2n} = V_n^2 - 2Q^n\,

Cas particuliers

Les suites de Lucas ont des noms spécifiques pour certaines valeurs de P et Q :

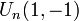U_n(1,-1)\, est appelée suite de Fibonacci, et ses valeurs sont les nombres de Fibonacci.
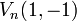V_n(1,-1)\, est une suite de Lucas, dont les valeurs sont les nombres de Lucas.
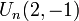U_n(2,-1)\, est appelée suite de Pell et ses valeurs sont les nombres de Pell.
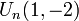U_n(1,-2)\, est appelée suite de Jacobsthal et ses valeurs sont les nombres de Jacobsthal.

Applications

Ce document provient de « Suite de Lucas ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Suite de lucas de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Suite de Lucas — En mathématiques, une suite de Lucas est une généralisation de la suite de Fibonacci et des nombres de Lucas. Les suites de Lucas furent étudiées en premier par le mathématicien français Édouard Lucas. Sommaire 1 Relations de récurrence 2 Terme… …   Wikipédia en Français

  • Suite de fibonacci — La suite de Fibonacci est une suite d entiers très connue. Elle doit son nom à un mathématicien italien connu sous le nom de Leonardo Fibonacci qui, dans un problème récréatif posé dans un de ses ouvrages, le Liber Abaci, décrit la croissance d… …   Wikipédia en Français

  • Suite de Fibonacci — La suite de Fibonacci est une suite d entiers très connue. Elle doit son nom à Leonardo Fibonacci, dit Leonardo Pisano, un mathématicien italien du XIIIe siècle qui, dans un problème récréatif posé dans un de ses ouvrages, le Liber Abaci,… …   Wikipédia en Français

  • Lucas van Leyden — Autoportrait Nom de naissance Lucas Huighensz Jacobsz Naissance 1494 Leyde Décès …   Wikipédia en Français

  • Lucas Pezzini Leiva — Lucas Situation actuell …   Wikipédia en Français

  • Lucas Grabeel — Nom Lucas Stephen Grabeel Naissance 23 novembre 1984 (1984 11 23) (26 ans) Springfield …   Wikipédia en Français

  • suite — [ sɥit ] n. f. • XIIIe; siute « poursuite en justice » 1080; a. p. p. de suivre; lat. pop. sequitus I ♦ A ♦ Action de poursuivre. 1 ♦ Dr. Droit de suite : droit qui permet au créancier hypothécaire de suivre l immeuble hypothéqué dans les mains… …   Encyclopédie Universelle

  • Lucas Arts — LucasArts Logo de LucasArts Dates clés 1982 : Création Personnages clés George Lucas …   Wikipédia en Français

  • Lucas Grabeel — Infobox Musician Name = Lucas Grabeel Img capt = Lucas Grabeel singing Bop to the Top in . Background = solo singer Birth name = Lucas Stephen Grabeel Born = birth date and age|1984|11|23 Springfield, Missouri agh| Genre = Pop Occupation = Actor …   Wikipedia

  • Suite (mathématiques) — Pour les articles homonymes, voir Suite. En mathématiques, une suite[1] est une famille d éléments indexée par les entiers naturels. Une suite finie est une famille indexée par les entiers strictement positifs inférieurs ou égaux à un certain… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”