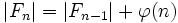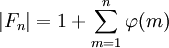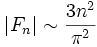Suite de farey

Suite de Farey

Pour les articles homonymes, voir Farey.

En mathématiques, la suite de Farey d'ordre n est la suite des fractions irréductibles entre 0 et 1 dont le dénominateur est inférieur ou égal à n et en ordre croissant.

Chaque suite de Farey commence avec la valeur 0, décrite par la fraction ⁰⁄₁, et finit avec la valeur 1, décrite par la fraction ¹⁄₁ (bien que certains auteurs omettent ces termes).

Une suite de Farey est quelquefois appelée série de Farey, ce qui n'est pas véritablement correct, les termes n'étant pas additionnés.

Exemples

Les suites de Farey d'ordre 1 à 8 sont :

F₁ = {⁰⁄₁, ¹⁄₁}

F₂ = {⁰⁄₁, ¹⁄₂, ¹⁄₁}

F₃ = {⁰⁄₁, ¹⁄₃, ¹⁄₂, ²⁄₃, ¹⁄₁}

F₄ = {⁰⁄₁, ¹⁄₄, ¹⁄₃, ¹⁄₂, ²⁄₃, ³⁄₄, ¹⁄₁}

F₅ = {⁰⁄₁, ¹⁄₅, ¹⁄₄, ¹⁄₃, ²⁄₅, ¹⁄₂, ³⁄₅, ²⁄₃, ³⁄₄, ⁴⁄₅, ¹⁄₁}

F₆ = {⁰⁄₁, ¹⁄₆, ¹⁄₅, ¹⁄₄, ¹⁄₃, ²⁄₅, ¹⁄₂, ³⁄₅, ²⁄₃, ³⁄₄, ⁴⁄₅, ⁵⁄₆, ¹⁄₁}

F₇ = {⁰⁄₁, ¹⁄₇, ¹⁄₆, ¹⁄₅, ¹⁄₄, ²⁄₇, ¹⁄₃, ²⁄₅, ³⁄₇, ¹⁄₂, ⁴⁄₇, ³⁄₅, ²⁄₃, ⁵⁄₇, ³⁄₄, ⁴⁄₅, ⁵⁄₆, ⁶⁄₇, ¹⁄₁}

F₈ = {⁰⁄₁, ¹⁄₈, ¹⁄₇, ¹⁄₆, ¹⁄₅, ¹⁄₄, ²⁄₇, ¹⁄₃, ³⁄₈, ²⁄₅, ³⁄₇, ¹⁄₂, ⁴⁄₇, ³⁄₅, ⁵⁄₈, ²⁄₃, ⁵⁄₇, ³⁄₄, ⁴⁄₅, ⁵⁄₆, ⁶⁄₇, ⁷⁄₈, ¹⁄₁}

Histoire

L'histoire des 'séries de Farey' est très curieuse — Hardy & Wright (1979) Chapitre III

... une fois encore, l'homme dont le nom fut donné à la relation mathématique n'était pas celui qui l'a découverte. — Beiler (1964) Chapitre XVI

Les suites de Farey furent nommées en l'honneur du géologue britannique, Sir John Farey. Sa lettre à propos de ces suites fut publiée dans le Philosophical Magazine en 1816. Farey conjectura que chaque terme dans une telle suite est le médian de ses voisins — néanmoins, à ce que l'on connaît, il ne prouva pas cette propriété. La lettre de Farey fut lue par Cauchy, qui donna la preuve dans ses Exercices de mathématique, et attribua ce résultat à Farey. En fait, un autre mathématicien, C. Haros, publia des résultats similaires en 1802 qui ne fut pourtant certainement pas autant connu que Farey ou Cauchy. Ainsi, c'est un accident historique qui relie le nom de Farey à ces suites.

Propriétés

Nombre de termes d'une suite de Farey

La suite de Farey d'ordre n contient tous les éléments des suites de Farey d'ordre inférieur. En particulier, F_n contient tous les éléments de la suite F_n−1, ainsi qu'une fraction supplémentaire pour chaque entier inférieur à n et premier avec n. Ainsi, la suite F₆ est composée des éléments de la suite F₅ auxquels il faut ajouter les fractions ¹⁄₆ et ⁵⁄₆. Le terme médian d'une suite de Farey est toujours ¹⁄₂, lorsque n > 1.

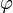Il est possible de relier le nombre de termes de F_n (noté $| F n |$ ) et celui de F_n−1 en utilisant l'indicatrice d'Euler $\varphi\,$ :

$|F_n| = |F_{n-1}| + \varphi(n)$

En utilisant le fait que |F₁| = 2, le nombre de termes de F_n peut donc s'exprimer en fonction de n de la façon suivante :

$|F_n| = 1 + \sum_{m=1}^n \varphi(m)$

Le comportement asymptotique de |F_n| est :

$|F_n| \sim \frac {3n^2}{\pi^2}$

Les voisins dans une suite de Farey

Les fractions qui sont des termes voisins dans une suite de Farey ont les propriétés suivantes.

Si ^a⁄_b et ^c⁄_d sont voisins dans une suite de Farey, avec ^a⁄_b < ^c⁄_d, alors leur différence ^c⁄_d − ^a⁄_b est égale à ¹⁄_bd. Comme

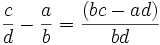$\frac{c}{d}-\frac{a}{b}=\frac{(bc-ad)}{bd}$ ,

il est équivalent de dire ceci

bc − ad = 1.

Ainsi ¹⁄₃ et ²⁄₅ sont voisins dans F₅, et leur différence est ¹⁄₁₅.

L'inverse est également vrai. Si

bc − ad = 1

pour les entiers naturels a,b,c et d avec a < b et c < d alors ^a⁄_b et ^c⁄_d sont voisins dans la suite de Farey dans l'ordre max(b,d).

Si ^p⁄_q possèdent des voisins ^a⁄_b et ^c⁄_d dans certaines suites de Farey, avec

^a⁄_b < ^p⁄_q < ^c⁄_d

alors ^p⁄_q est le médian de ^a⁄_b et ^c⁄_d — en d'autres mots,

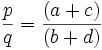$\frac{p}{q}=\frac{(a+c)}{(b+d)}$ .

Et, si ^a⁄_b et ^c⁄_d sont voisins dans une suite de Farey alors le premier terme qui apparaît entre eux lorsque l'ordre de la suite de Farey est augmenté est

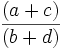$\frac{(a+c)}{(b+d)}$ ,

lequel apparaît en premier dans la suite de Farey d'ordre b+d.

Ainsi, le premier terme apparaissant entre ¹⁄₃ et ²⁄₅ est ³⁄₈, qui apparaît dans F₈.

L'arbre de Stern-Brocot est une structure de données montrant comment la suite est construite à partir de 0 (= ⁰⁄₁) et 1 (= ¹⁄₁), en prenant les médians successifs.

Les fractions qui apparaissent comme voisines dans une suite de Farey ont des développements en fraction continue reliés. Si ^p⁄_q admet le développement en fraction continue

[0; a 1, a 2,..., a n - 1, a n,1]

alors les deux voisins les plus proche de ^p⁄_q dans F_q ont pour développement en fraction continue

[0; a 1, a 2,..., a n - 1, a n]

[0; a 1, a 2,..., a n - 1]

Ainsi ³⁄₈ a pour développement en fraction continue [0;2,1,1,1], et ses voisins dans F₈ sont ²⁄₅ qui admet le développement $[0;2,1,1]$ et ¹⁄₃ qui être développé en [0;2,1].

Article détaillé : Arbre de Stern-Brocot.

Cercles de Ford

Il existe une relation intéressante entre les suites de Farey et les cercles de Ford.

Pour toute fraction (réduite) p/q il existe un cercle de Ford C[p/q], qui est le cercle de rayons 1/2q² et de centre (p/q,1/2q²). Les cercles de Ford correspondant à deux fractions distinctes sont soit disjoints soit tangents - deux cercles de Ford ne peuvent pas être sécants. Si 0<p/q<1, alors les cercles de Ford qui sont tangents à C[p/q] sont précisément les cercles de Ford associés aux fractions qui sont voisines de p/q dans une suite de Farey.

Ainsi C[2/5] est tangent à C[1/2], C[1/3], C[3/7], C[3/8], etc.

Article détaillé : Cercle de Ford.

Hypothèse de Riemann

Les suites de Farey sont utilisées dans deux formulations équivalentes de l'hypothèse de Riemann. Supposons que les termes de 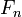$F_n\,$ soient 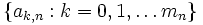$\{a_{k,n} : k = 0, 1, \ldots m_n\}\,$ . Définissons 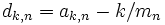$d_{k,n} = a_{k,n} - k/m_n\,$ , en d'autres mots $d k, n$ est la différence entre le k-ème terme de la n-ème suite de Farey, et le k-ème membre d'un ensemble de même nombre de points, distribués également sur l'intervalle unité. Franel et Landau ont démontré que chacun des deux énoncés :

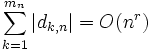$\sum_{k=1}^{m_n} |d_{k,n}| = O(n^r)$ pour tout r>1/2, et

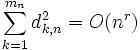$\sum_{k=1}^{m_n} d_{k,n}^2 = O(n^r)$ pour tout r>1,

est équivalent à l'hypothèse de Riemann.

Article détaillé : Hypothèse de Riemann.

Un algorithme simple

De manière surprenante, un algorithme simple existe pour engendrer les termes dans un ordre, soit traditionnel (ascendant), soit non-traditionnel (descendant) :

 100   'Code UBASIC pour engendrer une Suite de Farey d'ordre N dans l'ordre traditionnel
 110   N=7:NumTerms=1
 120   A=0:B=1:C=1:D=N
 140   print A;B
 150   while (C<N)
 160      NumTerms=NumTerms+1
 170      K=int((N+B)/D)
 180      E=K*C-A:F=K*D-B
 190      A=C:B=D:C=E:D=F:print A;B
 200   wend
 210   print NumTerms
 220   end

Cet algorithme se déduit du fait que, si $a / b$ et $c / d$ sont deux termes successifs dans une suite de Farey alors les successeurs de $c / d$ sont tous de la forme $(k c - a) / (k d - b)$ . Pour trouver le successeur à l'ordre $n$ il faut trouver le plus grand $k$ tel que 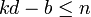$kd - b \leq n$ et celui-ci est fourni par la partie entière du quotient de $n + b$ par $d$ .

Pour engendrer la suite dans un ordre descendant (non-traditionnel) :

 120   A=1:B=1:C=N-1:D=N
 150   while (A>0)

Des recherches en force brute pour les solutions d'équations diophantiennes rationnelles peuvent souvent prendre l'avantage sur les suites de Farey (pour chercher seulement celles en formes réduites); la ligne 120 peut aussi être modifiée pour inclure deux termes adjacents quelconques afin d'engendrer seulement les termes plus grands (ou plus petits) qu'un terme donné.

Références

Beiler, Albert H. (1964) Recreations in the Theory of Numbers (Second Edition). Dover. ISBN 0486210960

(en) G. H. Hardy et E. M. Wright An Introduction to the Theory of Numbers [détail des éditions]

Liens externes

(en) Suites de Farey
(en) Page MathWorld sur les arbres de Stern-Brocot

Portail des mathématiques

Ce document provient de « Suite de Farey ».

Catégories : Fraction | Arithmétique | Suite

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Suite de farey de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Suite de Farey — Pour les articles homonymes, voir Farey. En mathématiques, la suite de Farey d ordre n est la suite des fractions irréductibles entre 0 et 1 dont le dénominateur est inférieur ou égal à n et en ordre croissant. Chaque suite de Farey commence avec … Wikipédia en Français
Farey — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Patronyme Le nom de Farey est porté par plusieurs personnalités (par ordre alphabétique) : John Farey (1766 1826), géologue et mathématicien… … Wikipédia en Français
John Farey (1766-1826) — Pour les articles homonymes, voir John Farey. John Farey au Derby Museum. Cette silhouette a été réalisé par son ami White Watson et le QR Code que l on peut vo … Wikipédia en Français
John farey (1766-1826) — Pour les articles homonymes, voir John Farey. John Farey (1766 – 6 janvier 1826) est un géologue et écrivain anglais né à Woburn dans le Bedfordshire. Cauchy donna son nom à une suite mathématique connue comme suite de Farey qu il avait… … Wikipédia en Français
Arbre de Stern-Brocot — En mathématiques, l arbre de Stern Brocot est une représentation de tous les rationnels strictement positifs, sous forme de fractions irréductibles. Il a été découvert presque simultanément par le mathématicien allemand Moritz Stern (en)… … Wikipédia en Français
NOMBRES (THÉORIE DES) - Théorie analytique — Ce qu’on appelle la «théorie analytique des nombres» ne peut pas être considéré comme une théorie mathématique au sens usuel qu’on donne à ces mots, c’est à dire un système organisé de définitions et de théorèmes généraux accompagné… … Encyclopédie Universelle
Fonction zêta de Riemann — La fonction zêta de Riemann ζ(s) dans le plan complexe. La couleur d un point s code la valeur de ζ(s) : des couleurs vives indiquent des valeurs proches de 0 et la nuance indique l argument de la valeur. Le point blanc pour s = 1… … Wikipédia en Français
Arbre De Stern-Brocot — En mathématiques, un arbre de Stern Brocot est une représentation de toutes les fractions irréductibles strictement positives. Cet arbre constitue une manière plutôt élégante de construire l ensemble des rationnels . Il a été découvert… … Wikipédia en Français
Arbre de stern-brocot — En mathématiques, un arbre de Stern Brocot est une représentation de toutes les fractions irréductibles strictement positives. Cet arbre constitue une manière plutôt élégante de construire l ensemble des rationnels . Il a été découvert… … Wikipédia en Français
Fonction Zeta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Suite de farey

Suite de Farey

Sommaire

Exemples

Histoire