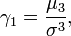- Asymétrie (skewness)
-
Asymétrie (statistique)
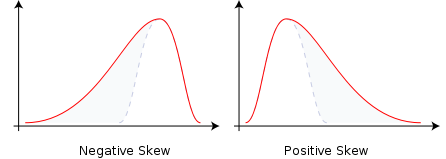
En théorie des probabilités et statistiques, le coefficient de dissymétrie (skewness) est un moment standardisé qui mesure l'asymétrie de la densité de probabilité d'une variable aléatoire définie sur les nombre réels. En termes généraux, l'asymétrie d'une distribution est positive si la queue de droite (à valeurs hautes) est plus longue ou grosse, et négative si la queue de gauche (à valeurs basses) est plus longue ou grosse.
L'asymétrie est le troisième moment standardisé, se note γ1 et est calculé à partir du cube des écarts à la moyenne et mesure le manque de symétrie d'une distribution.
Où μ3 est le troisième moment centré et σ est l'écart-type.
- Un coefficient positif indique une distribution étalée vers la gauche, et donc une queue de distribution étalée vers la droite;
- Un coefficient négatif indique une distribution étalée vers la droite, et donc une queue de distribution étalée vers la gauche;
- Dans le cas d'une distribution normale, par symétrie on a: γ1 = 0. La distribution est symétrique.
Moments
Article détaillé : moment (mathématiques).Les moments d'une variable aléatoire X permettent de caractériser sa distribution. On définit notamment le moment d'ordre r :
Le moment d'ordre r = 1 est l'espérance mathématique ou moyenne de la variable aléatoire X.
On définit également un moment centré µ par rapport à la moyenne m d'une population. On appelle variance de la population le moment centré du second ordre. Selon Pearson, les quatre moments m, µ1, µ2 et µ4 suffisent à définir la plupart des distributions continues.Estimateur non biaisé
La définition théorique γ1 du coefficient d'asymétrie est une mesure biaisé de l'asymétrie de la population. Un estimateur non biaisé de l'asymétrie est donné par la formule :
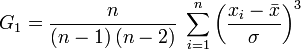
avec σ un estimateur non biaisé de la variance.
Articles connexes
- Portail des probabilités et des statistiques
Catégories : Probabilités | Statistique descriptive
Wikimedia Foundation. 2010.