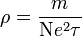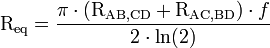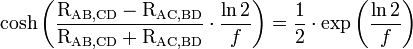- Résisistivité
-
Résistivité
La résistivité d'un matériau, généralement symbolisée par la lettre grecque rho (ρ), représente sa capacité à s'opposer à la circulation du courant électrique. Elle correspond à la résistance d'un tronçon de matériau de 1 m de longueur et de 1 m2 de section ; elle est exprimée en ohm-mètre (Ω·m). On utilise aussi :
- le Ω·mm2/m = 10-6 Ω·m ;
- le μΩ·cm = 10-8 Ω·m.
La résistance R (en ohms) d'une pièce rectiligne de longueur L (en mètres) et de section droite d'aire S (en mètres carrés) vaut donc :
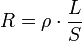 .
.C'est la grandeur inverse de la conductance électrique (symbole : G).
La résistivité des matériaux dépend de la température :
- Pour les métaux, à la température ambiante, elle croit linéairement avec la température. Cet effet est utilisé pour la mesure de température (sonde Pt 100)
- Pour les semi-conducteurs, elle décroît fortement avec la température, la résistivité peut aussi dépendre de la quantité de rayonnement (lumière visible, infra-rouge, etc.), absorbé par le composant.
Sommaire
Résistivités usuelles
Matériaux
Nom du métal Résistivité à 300 K
(Ω·m)Argent 16·10-9 Cuivre 17·10-9 Or 22·10-9 Aluminium 27·10-9 Magnésium 46·10-9 Bronze 50·10-9 Zinc 60·10-9 Nickel 70·10-9 Laiton 70·10-9 Cadmium 76·10-9 Platine 94·10-9 Fer 104·10-9 Étain 142·10-9 Plomb 207·10-9 Germanium 460·10-9 Constantan 500·10-9 Mercure 960·10-9 Nichrome 1000·10-9 Carbone 35 000·10-9 L'argent métallique est le corps pur simple qui est le meilleur conducteur d'électricité à température ambiante.
Isolants
nom du matériau résistivité (Ω·m) eau distillée 109 verre 1017 air variable polystyrène 1020 Calcul de la résistivité des cristaux
Dans le cas d'un cristal parfait, on peut calculer la résistivité en fonction des paramètres fondamentaux[1].
Cristaux covalents
Les cristaux covalents sont des isolants, la bande interdite est large. Avec l'élévation de température, des électrons peuvent être suffisamment excités pour franchir le gap. La conductivité suit donc une loi en
- T3/2exp(-Eg/kT)
où
- T est la température absolue ;
- Eg est la largeur de la bande interdite ;
- k est la constante de Boltzmann.
Cristaux ioniques
Dans les cristaux ioniques, la conduction se fait par migration de défauts. Le nombre et la mobilité des défauts suivent une loi d'Arrhénius, la conductivité suit donc une loi similaire, en
- exp(-Q/RT)
où
- Q est l'énergie de formation ou de migration des défauts ;
- R est la constante des gaz parfaits ;
- T est la température absolue.
Article détaillé : Conduction électrique dans les oxydes cristallins.Cristaux métalliques
Dans le cas des cristaux métalliques, la résistivité augmente avec la température ; la conductivité augmente linéairement avec T. Cela est dû à l'interaction entre les électrons et les phonons.
Le premier modèle utilisé considère que les électrons se comportent comme un gaz, le libre parcours moyen des électrons étant déterminé par les chocs avec les ions (atomes du réseau sans leurs électrons libres, réseau appelé « gellium »). On trouve une résistivité valant
avec
- m : masse d'un électron ;
- N : nombre d'électrons par unité de volume, de l'ordre de 1028 m-3 ;
- e : charge élémentaire ;
- τ : temps de relaxation, c'est-à-dire durée moyenne séparant deux collisions.
Mais ce modèle ne prend pas en compte l'effet de la température ni des impuretés.
Selon la relation de Matthiessen, la conductivité comprend trois composantes :
- ρ = ρT + ρi + ρD
avec
- ρT : contribution de l'agitation thermique ;
- ρi : contribution des impuretés, de l'ordre du μΩ⋅cm/% d'impureté ;
- ρD : contribution des défauts atomiques.
Le modèle de Drude prend en compte l'effet Joule, c'est-à-dire l'énergie cinétique que les électrons cèdent au réseau à chaque collision. Comme les autres modèles, c'est un modèle non quantique, qui permet également de prévoir la conductivité thermique, mais décrit mal ce qui se passe pour les températures très basses.
La résistivité d'un métal à une température proche de l'ambiante est en général donnée par :
- ρ = ρ0(1 + αθ)
avec
- ρ0 : résistivité à 0 °C ;
- α : coefficient de température (K-1) ;
- θ : température en degrés Celsius.
Coefficients de température de quelques métaux[2] Métal α (10-3K-1) Argent 3,85 Cuivre 3,93 Aluminium 4,03 Plomb 4,2 Nickel 5,37 Fer 6,5 Tungstène 45 Mesure de la résistivité
Résistivité des sols
Article détaillé : Terre (électricité).On utilise un telluromètre et la méthode de Wenner :
On plante 4 piquets alignés et équidistants notés 1, 2, 3 et 4. Le courant de mesure est injecté entre les piquets 1 et 4 et la résistance est mesurée entre 2 et 3. Si la distance entre 2 piquets est égale à D, la résistivité du sol se calcule avec la formule :
- ρ = 2π⋅D⋅R23.
Résistivité des couches minces
La méthode 4 pointes ou méthode de Van der Pauw est utilisable pour mesurer la résistivité d’une couche mince. Il faut placer les 4 pointes près des bords de la couche à caractériser.
Soit un rectangle dont les côtés sont numérotés de 1 à 4 en partant du bord supérieur, et en comptant dans le sens des aiguilles d'une montre. On injecte le courant entre deux points du bord 1 et on mesure la tension entre les deux points du bord opposé (bord 3). Le rectangle pouvant ne pas être strictement un carré nous effectuons une deuxième mesure en injectant cette fois ci le courant entre les deux points du bord 4, et comme précédemment nous mesurons ensuite la tension entre les deux points du bord opposé (bord 2). Il suffit ensuite de calculer à l’aide de la loi d'Ohm, le rapport V/I pour chaque configuration de mesures.
Nous obtenons ainsi RAB,CD et RAC,BD.
La résistivité ρ est la solution de l'équation dite équation de Van der Pauw :
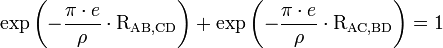 .
.
où e est l'épaisseur de la couche.
Une méthode de résolution consiste à calculer la résistance équivalente par la formule suivante :
ƒ étant le facteur de forme obtenu d’après la relation :
Nous calculons ensuite la résistivité avec :
- ρ = Req⋅e.
Notes
Voir aussi
- Portail de la physique
- Portail de l’électricité et de l’électronique
Catégorie : Théorie électrique
Wikimedia Foundation. 2010.