Règle à calcul

Règle à calcul scolaire de 10 pouces (Pickett N902-T simplex trig).

La règle à calcul (ou règle à calculer) est un instrument mécanique de calcul analogique qui permet, par simple déplacement longitudinal d’échelles graduées, d’effectuer directement des opérations arithmétiques de multiplication et de division, mais pas les additions ni les soustractions. Une règle à calcul peut aussi servir à exécuter des opérations plus complexes, telles que le calcul de racines carrées ou cubiques, des calculs logarithmiques ou bien trigonométriques^[1].

Avant l'apparition des calculatrices électroniques vers 1970, les règles à calcul étaient extrêmement utilisées par les scientifiques, les ingénieurs et étudiants^[2]. En effet, elles apportaient une aide appréciable pour

• les calculs approchés qui, avec l’entraînement, pouvaient être exécutés rapidement.
• la détermination des valeurs complexes comme les logs ou la trigonométrie sans avoir recours à une table.

Considérées comme obsolètes de nos jours, la plupart sont devenues des articles de collection. Des règles à calcul circulaires sont, toutefois, encore utilisées pour la navigation aérienne, ainsi que sur les cadrans à lunette tournante de certaines montres.

Composants

Curseur d’une règle à calcul

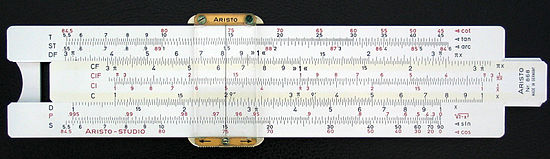
• Une règle à calcul se compose en général de deux réglettes fixes solidaires graduées, dans lesquelles s’imbrique une réglette mobile, également graduée, ainsi que d’un curseur se déplaçant longitudinalement. Les plus beaux modèles sont totalement double face, étant constitués de deux règles reliées par des ponts, encadrant une réglette mobile, ce qui permet l'utilisation d'un plus grand nombre d'échelles.
• La réglette centrale peut coulisser par rapport aux deux autres, et permet de décaler des graduations. Elle est souvent graduée des deux côtés : d’un côté X²y , X³ , 1/X , Xy et de l’autre les fonctions trigonométriques.
• Le curseur central facilite la lecture et l’interpolation entre les graduations ; il sert surtout à mémoriser une valeur, lors de calculs enchaînés (règle de trois par exemple).
• Il existe aussi des versions circulaires (cercle à calcul) ou hélicoïdales (hélice à calcul).

Principe

Détermination des différentes échelles

Règle proposant, sur cette face et dans l'ordre, les échelles LL1, A, B, T, S, C, D, LL2

La composition des règles à calcul est variable. Il convient donc à l'utilisateur de repérer les échelles.

• On trouve souvent quatre échelles étiquetées A, B, C et D. A et B sont des carrés (identifiables par une graduation logarithmique de 1 à 100), C et D les unités (graduation logarithmique de 1 à 10). L'échelle B est souvent absente. Dans ce cas, on peut juste trouver les carrés et racines carrées, mais pas calculer dans les carrés. Pour reconnaître avec certitude une échelle des carrés, il s'agit de deux échelles identiques graduées de 1 à 10 mises bout-à-bout. Le premier 10 est exactement au milieu de la règle.
• On trouve aussi presque toujours une échelle des cubes (graduée de 1 à 1000) : trois échelles logarithmiques identiques bout-à-bout
• On trouve généralement une échelle de logs (décimaux), graduée de 0 à 10 et qui n'est pas logarithmique, mais tout à fait régulière.
• Un grand classique est l'échelle des inverses : elle est identique aux échelles C et D des unités, mais de droite à gauche. Souvent notée CI et graduée en rouge.
• Encore presque toujours, les fonctions trigonométriques : S pour les sinus (gradués de 6 à 90), T pour les tangentes (graduées de 6 à 45)
• Sur les règles modernes, les échelles Log-Log, notées LL
• Sur les règles spécialisées (électricité, etc.), des échelles dédiées à des calculs spécifiques. On les identifiera grâce à la documentation, aux inscriptions situées dans les marges et à une bonne connaissance du domaine en question.

Utilisation des échelles pour les calculs

Multiplication et division

Multiplication de 2x3 (en fait, toute la table des 2 jusqu'à 5)

Multiplication de 2 par les nombres plus grands que 5

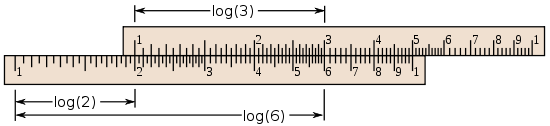
Pour son utilisation la plus courante (la multiplication et la division), la règle à calcul utilise des échelles logarithmiques et le principe selon lequel la somme des logarithmes de deux nombres est égale au logarithme du produit des deux nombres:

log (a) + log (b) = log (a × b).

Cela se traduit par le fait que, pour multiplier deux valeurs, il suffit d’additionner leurs longueurs représentées sur la règle, et de les retrancher pour faire une division.

On positionne donc le 1 de la règle mobile en regard du 2 de la règle fixe, et on lit le résultat 6 sur l'échelle fixe en face du 3 de la règle mobile.

Cette opération est très facile à effectuer, mais a l’inconvénient de ne pas donner les exposants de 10 (la position de la virgule), qui doivent être trouvés par une autre méthode (généralement un calcul mental approché).

Un autre inconvénient est que le résultat est souvent hors échelle (par exemple, 2x6 est impossible sur le premier exemple). Dans ce cas, on procède comme sur le deuxième exemple, en alignant le nombre à multiplier, non pas avec le 1, mais avec le 10 (deuxième exemple).

Échelles CF-DF. On constate que 1,3x8 tombe hors échelle, mais fonctionne si on cherche le résultat sur CF (10,4 environ)

Pour limiter cet inconvénient, certaines règles proposent un petit prolongement au bout de chaque échelle, ou bien des échelles décalées notées CF et DF, allant de racine de 10 à racine de 10, avec le 1 au milieu. Dans ce cas, on commence le calcul sur l'échelle classique C-D, et on le finit sur CF-DF.

Pour la division, la position des règles est la même que pour la multiplication. L'exemple illustré ci-dessus concerne aussi bien la division de 6 par 3 : en retranchant la longueur (log) de 3 à la longueur 6, on obtient la longueur 2.

Calculs enchaînés

Lorsque l'on vient de faire une division le 1 de l'échelle C est placé en face du résultat, et est idéalement positionné pour faire une multiplication de ce nombre par un autre.

Une fois ce nouveau nombre trouvé, on le repère grâce au curseur mobile, et on déplace la règle mobile pour placer le nouveau diviseur en face du repère pour obtenir une nouvelle division, et ainsi de suite.

On constate donc qu'on peut alterner à l'infini des multiplications et des divisions avec un minimum de déplacements des éléments de la règle.

Carrés, cubes et racines

La racine carrée de 2,1

Les règles à calcul servent aussi à trouver les carrés, les cubes, ainsi que les racines.

Le maniement est très simple. Généralement, il suffit d'utiliser le curseur et de chercher la correspondance sur l'échelle adaptée.

Pour trouver le carré d'un nombre, on place le curseur sur ce nombre sur l'échelle des unités, et on cherche son correspondant sur l'échelle des carrés. En procédant à l'inverse, on trouve, sur l'échelle des unités, la racine carrée d'un nombre lu sur l'échelle des carrés. L'exemple ci-contre montre aussi bien que la racine carrée de 2,1 (échelle A) est proche de 1,45 (échelle D), que l'inverse.

Le principal piège est de ne pas se tromper dans le choix du nombre pour une racine carrée : la racine carrée de 9 est 3, tandis que celle de 90 est d'environ 9,5. En revanche, si l'on cherche la racine de 900, on doit bien trouver bien 30. En pratique, il faut donc trouver combien de fois on peut retirer deux zéros pour arriver à un nombre entre 1 et 100 pour choisir la position sur l'échelle.

On procède exactement pareil pour les cubes et racines cubiques, simplement en utilisant l'échelle des cubes au lieu de l'échelle des carrés.

Inverses

L'échelle CI donne les inverses de l'échelle C (ou D). Il est facile de constater, en déplaçant le curseur que 5 est en face de 2 (1/2 = 0,5) et inversement.

Cette échelle semble faire double emploi au premier abord avec les échelles C et D. En effet, pour trouver l'inverse de 5, il suffit de diviser 10 par 5 pour trouver 2.

En fait, cette échelle permet un gain de temps notable pour les calculs à la chaîne. En effet, nous avons vu qu'il est très rapide d'alterner des multiplications et divisions avec un minimum de déplacements. Dans le cas où l'on aurait plusieurs multiplications à enchaîner, il suffit de considérer une multiplication sur deux comme une division par l'inverse.

Trigonométrie

Règle avec échelles S, ST, T1 et T2 sur la face principale

Les sinus sont de lecture simple : après repérage de l'échelle des sinus (souvent au dos de la règle mobile), on place le curseur sur l'angle désiré, et on trouve le sinus sur l'échelle D (penser à placer la virgule, en pensant qu'il s'agit d'un nombre entre 0 et 1, ce qui pose d'ailleurs un problème, puisque la règle donne des résultats de 0,1 à 1). Par exemple, le sinus de 45 devrait se trouver proche du chiffre 7.

Les sinus des petits angles (<6°, soit un sinus < 0,1, représentant le début de l'échelle D) nécessitent une échelle supplémentaire ST.

Les cosinus sont les sinus des angles complémentaires. Par exemple, le cosinus de 60° est le sinus de 30°. On se passe donc d'échelle des cosinus moyennant un calcul simple.

Les tangentes s'utilisent comme les sinus, à ceci près que l'échelle des tangentes s'arrête à 45° (la tangente de 45° est 1, ce qui est la limite de l'échelle D). N'oublions pas que les tangentes tendent vers l'infini lorsque les angles approchent de 90°. Certaines règles proposent une échelle T2 pour les grands angles

Enfin, les cotangentes sont de même valeur que les tangentes des angles complémentaires à 90°.

Logarithmes

Les règles à calcul comportent le plus souvent une échelle de logarithmes en base 10, sur la face avant ou arrière de la règle selon les cas.

Après identification de l'échelle (une échelle de 0 à 1 sur laquelle les chiffres sont régulièrement espacés et étiquetée L), on repère la correspondance entre l'échelle de base (notée D en général) avec l'échelle des logs.

Pour mémoire, le log est la partie décimale du nombre qu'il faut mettre en exposant à 10 pour obtenir une certaine valeur.

Par exemple, 10^0,2 vaut environ 3. Le 2 de l'échelle D doit donc correspondre au 3 de l'échelle des logs.

Lecture

La lecture des échelles est un peu déroutante pour les débutants.

En effet, le nombre de graduations entre les chiffres n'est généralement pas constant d'un bout à l'autre de l'échelle, car les espaces changent, et on ne peut tasser indéfiniment les graduations au fur et à mesure que les chiffres se resserrent.

De plus, certaines échelles se lisent de gauche à droite, tandis que les autres se lisent de droite à gauche.

Comme pour compliquer tout cela, les zéros sont souvent sous-entendus, ce qui fait que, par exemple, sur l'échelle des cubes, parfois les puissances de 10 ne sont pas notées 10-100-1000, mais 1-1-1.

Enfin, il y a peu d'indications sur l'usage des échelles.

L'utilisateur doit donc utiliser son bon sens pour

• déterminer le sens de lecture (les inverses se lisent de droite à gauche)
• compter les graduations pour savoir si un trait vaut 0,1 (9 graduations entre deux chiffres), 0,2 (4 graduations) ou 0,5 (1 graduation)
• déterminer l'amplitude de l'échelle (unités de 1 à 10, carrés de 1 à 100, cubes de 1 à 1 000, par exemple), afin de ne pas confondre 2 et 20, par exemple
• déterminer l'usage de chaque échelle (en s'aidant de l'aspect de l'échelle et des inscriptions souvent situées aux extrémités)

Précision et exactitude

La précision d’une règle dépend de sa longueur mais aussi de la qualité de la gravure.

Les règles de 30 cm donnent une précision de l’ordre de 1/200^e. Ce qui se traduit par deux décimales au voisinage de la valeur 2. La différence du nombre de décimales visibles en fonction de la valeur, n’est qu’un simple effet d’échelle.

La qualité de gravure est primordiale pour la précision : les traits doivent être d'épaisseur identique sur toute la longueur de l'échelle, le plus fins possible.

Certaines règles sont fausses, ce qui peut être facile à démontrer, comme dans le cas où les échelles C et D ne sont pas strictement superposables.

Avant d'utiliser une règle inconnue pour des calculs importants, il peut être utile de la tester sur quelques calculs dont les résultats sont connus, et tombent juste de préférence.

Construction

Il est possible d’utiliser toutes sortes de matériaux, mais, à l’époque moderne, on utilisait surtout le plastique en Occident et le bambou en Orient.

L’os et l’ivoire ont été beaucoup employés.

Histoire

On aurait retrouvé une règle à calcul (plutôt un cercle à calcul) datant de l’antiquité romaine^[3].

Cercle à calcul pour calcul de temps de pose pour tirage photo

Cercle à calcul sur une montre de navigation aérienne

John Neper invente en 1614 les logarithmes, bases mathématiques de certaines fonctions des règles à calcul.

Edmund Gunter (1581-1626) enseignait alors l’astronomie au collège de Gresham. On lui doit l’invention de plusieurs instruments géométriques, tels que le secteur à l’aide duquel on trace les lignes parfaites des cadrans solaires. Il invente l’échelle dite "de Gunter" ou règle logarithmique en 1620, qui simplifie les opérations de calcul : sur cette règle, il suffisait d'ajouter ou retirer un écart à l'aide d'un compas pour multiplier ou diviser un nombre par un facteur.

Pour simplifier cette opération, Edmond Wingate, en 1627, a l'idée de faire coulisser deux échelles séparées^{[réf. souhaitée]}, l'une contre l'autre, donnant naissance au concept de la règle à calcul.

L’anglais William Oughtred invente en 1630 une règle à calcul circulaire, en transposant l'idée de Wingate sous la forme de deux échelles logarithmiques dessinées sur deux cercles concentriques.

M. Milburne, vers 1670, trace les premières spirales logarithmiques. Une version moderne et aboutie est réalisée et commercialisée en France par Léon Appoullot vers 1930.

En 1654, Robert Bissaker fait prendre à l’instrument sa forme classique (baguette coulissante dans une forme fixe).

Certains attribuent le montage des deux règles à Seth Partridge. Une description de la version Partridge est donnée dans The description and use of an instrument called the double scale of proportion, ouvrage de Partridge - London 1671, existant à la Bibliothèque Nationale.

Amédée Mannheim, officier puis professeur à l'École Polytechnique lui adjoint (1850) un pointeur mobile (curseur) permettant une lecture plus aisée et de « stocker » un résultat intermédiaire. La règle de type Mannheim est la première règle moderne.

L’enroulement de deux longues échelles logarithmiques sur un cylindre permit d’obtenir une précision de calcul théoriquement supérieure - Otis King en Angleterre, A. Lafay en France, tous deux vers 1921, puis Fuller. L'aspect confus et peu lisible de ces hélices logarithmiques a été cause de leur insuccès.

Vers 1950, André Séjourné, professeur en classe préparatoire aux Arts et Métiers au lycée Voltaire à Paris, perfectionne la règle à calcul normale en lui adjoignant les échelles LL1,LL2,LL3. C'est la règle à calcul Log-Log.

Les échelles Log-Log étaient déjà connues dans l'entre-deux-guerres, règle « Electro » avec LL2 et LL3 dès les années 1920, règle « Darmstadt » avec LL1, LL2 et LL3 en 1935. André Séjourné diffusa l'« Electro Log Log » (Graphoplex 640), qui ne fut utilisée pratiquement qu'en France.

La règle à calcul se diffusa en France à partir de la fin de la Seconde Guerre mondiale, les marques françaises les plus répandues étaient Tavernier-Gravet, Graphoplex et parmi les règles importées, les Nestler, Aristo et Faber-Castell allemandes, les Sun Hemmi japonaises en bambou et les Pickett américaines en aluminium. Son règne se poursuivit jusqu’au milieu des années 1980 malgré l’apparition des premières calculatrices, la règle étant le seul instrument autorisé lors des examens et concours. La circulaire du 28 juillet 1986, autorisant et recommandant l’emploi des calculettes pendant les épreuves des examens, la relégua finalement au fond des tiroirs. Elle est cependant toujours autorisée en 2011 au Concours commun Mines-Ponts^[4] et au concours de l'École polytechnique^[5].

Les règles à calcul subsistent encore dans certains métiers, comme la navigation aérienne. Certains appareils de mesures analogiques spécialisés (par exemple les posemètres) sont également équipés d’un cercle à calcul intégré pour faciliter l’utilisation des mesures.

Voir aussi

Voir aussi

• Astrolabe
• Nomogramme
• Abaque
• Machine d'Anticythère
• Les deux articles du wikilivre de photographie consacrés aux logarithmes et à leurs applications.

Sources

• L’ère de la règle à calcul, C Stoll, Pour la science, sept 2006, p12-17

Bibliographie

• R. Dudin, La Règle à calcul, Paris, Dunod, 1963, 212 p.
  Livre entièrement consacré à l'utilisation de la règle à calcul.
   

Liens externes

• De l’Utilisation d’une Règle à Calcul Principes de fonctionnement d’une règle à calcul.
• (en) Virtual Sun-Hemmi 153 Slide Rule Un émulateur de règle à calcul.
• (en) Eric’s Slide Rule Site
• (en) The Oughtred society Regroupe collectionneurs et amateurs de règles à calculs.
• Linealis.org L'un des seuls sites francophones sur les règles à calcul et en particulier sur la marque Graphoplex.
• photocalcul Un site francophone sur les règles à calcul et les instruments de calcul anciens
• (es) reglas de cálculo Un site espagnol avec la plus importante collection de règles FABER CASTELL du Net

• Portail des mathématiques