Assemblage (mathematiques)

Assemblage (mathematiques)

Assemblage (mathématiques)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Assemblage.

La notion d'assemblage s'utilise en Mathématiques dans l'analyse combinatoire.

Dans un ensemble fini E de cardinal n l'assemblage est constitué d'éléments de E.

Soit par exemple un ensemble E de cardinal 3 et composé des éléments x, y, z.

Les assemblages de taille 2 sont : xy, yz, yx, zz.

Il existe quatre types d'assemblages :

Assemblages ordonnés avec répétition

Soit un ensemble E de n éléments :il est possible de former 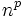n^p\, assemblages ordonnés avec répétition de taille p.

  • Exemple : x, y, z donnent neuf assemblages de ce type : xx, xy,xz ,yx ,yy ,yz ,zx ,zy ,zz.

(Voir également Arrangement avec répétition.)

  • Exemple : le tiercé dans l'ordre est un Assemblage ordonné sans répétition.

Assemblages non ordonnés sans répétition

Il s'agit en fait des Combinaisons.

  • Exemple : le tiercé dans le désordre est un Assemblage non ordonné sans répétition.

Assemblages non ordonnés avec répétition

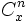C_x^n avec x= n+p-1 qui sont une forme particulière de combinaisons.

Il y a en effet autant d'assemblages de ce type que de combinaisons de n-1 éléments tirés parmi n+p-1 éléments.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Assemblage (math%C3%A9matiques) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Assemblage (mathematiques) de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Assemblage (Mathématiques) — Pour les articles homonymes, voir Assemblage. La notion d assemblage s utilise en Mathématiques dans l analyse combinatoire. Dans un ensemble fini E de cardinal n l assemblage est constitué d éléments de E. Soit par exemple un ensemble E de… …   Wikipédia en Français

  • Assemblage (mathématiques) — Pour les articles homonymes, voir Assemblage. La notion d assemblage s utilise en Mathématiques dans l analyse combinatoire. Dans un ensemble fini E de cardinal n l assemblage est constitué d éléments de E. Soit par exemple un ensemble E de… …   Wikipédia en Français

  • Assemblage (mathématique) — Assemblage (mathématiques) Pour les articles homonymes, voir Assemblage. La notion d assemblage s utilise en Mathématiques dans l analyse combinatoire. Dans un ensemble fini E de cardinal n l assemblage est constitué d éléments de E. Soit par… …   Wikipédia en Français

  • MATHÉMATIQUES (FONDEMENTS DES) — Au sens premier et fort, le mot «fondement» désigne la base, jugée inébranlable, sur laquelle repose un corps d’énoncés, un système de connaissances, un complexe de croyances ou de conduites. «Reposer sur la base» signifie ici «trouver en elle à… …   Encyclopédie Universelle

  • Assemblage — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Assemblage », sur le Wiktionnaire (dictionnaire universel) Assemblage peut avoir plusieurs… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Logique (mathématiques) — Logique mathématique La logique mathématique est née à la fin du XIXe siècle de la logique au sens philosophique du terme. Ses débuts furent marqués par la rencontre entre deux idées nouvelles : la volonté chez Frege, Russell, Peano et… …   Wikipédia en Français

  • Proposition (mathematiques) — Proposition (mathématiques) Cet article court présente un sujet plus amplement développé ici : Calcul des propositions. Une proposition est un concept de base du langage mathématique. C est un assemblage de symboles que le mathématicien… …   Wikipédia en Français

  • Proposition (mathématiques) — Cet article court présente un sujet plus amplement développé ici : Calcul des propositions. Une proposition est un concept de base du langage mathématique. C est un assemblage de symboles que le mathématicien souhaite soit démontrer, soit… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”