Arrangement Avec Répétition

Arrangement avec répétition

Un arrangement avec répétition en mathématiques, se produit lorsque nous rangeons dans un certain ordre k objets, choisis parmi n objets discernables, chaque objet pouvant être répété, nous pouvons représenter les différents rangements par des k-uplets (ou des k-listes). Par exemple, quand nous tirons successivement avec remise k boules dans une urne contenant n boules numérotées de 1 à n, nous pouvons représenter ces tirages par des k-listes de boules ou par des applications de {1, 2, ..., k} dans l'ensemble des boules.

Il y a plusieurs définitions d'un arrangement avec répétition.

Définition :

Étant donnés un ensemble fini E de cardinal n (n ∈ ℕ^⁎) et k un entier naturel, un k-arrangement avec répétition d'éléments de E, ou arrangement avec répétition de n éléments pris k à k, est un k-uplet d'éléments de E. Un tel k-uplet est aussi appelé une k-liste d'éléments de E.

Définition :

Étant donnés un ensemble fini E de cardinal n (n ∈ ℕ^⁎) et k un entier naturel, un k-arrangement avec répétition d'éléments de E, est une application de {1, 2, ..., k} dans E.

Nombre d'arrangements avec répétition

Théorème :

Soient E un ensemble fini de cardinal n (n ∈ ℕ^⁎) et k un entier naturel. L'ensemble des arrangements avec répétition est fini et son cardinal est égal à n^k.

Démonstration :

Cas où un arrangement avec répétition est un kuplet.
L'ensemble des k-arrangements avec répétition de E n'est autre que E^k=E × E × E × ... × E (k fois) et

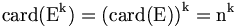$\rm{card}(E^k)=\left(\rm{card}(E)\right)^k=n^k$ .

Cas où un arrangement avec répétition est une application de {1, 2, ..., k} dans E.
Pour construire une application de {1, 2, ..., k} dans E, il suffit de
- choisir l'image de 1 et il y a n choix possibles,
- choisir l'image de 2 et il y a encore n choix possibles,
- etc.
- et enfin choisir l'image de k et il y a toujours n possibilités.

D'où au total n × n × ... × n=n^k applications différentes.

Exemple

En morse, les mots sont écrits avec un alphabet de deux symboles ─ et ●. Soit k un entier naturel non nul. Un mot de k lettres est un k-arrangement avec répétition de l'ensemble { ─ , ● }, donc il y a 2^k mots d'exactement k lettres.

Voir aussi

Portail des mathématiques

Ce document provient de « Arrangement avec r%C3%A9p%C3%A9tition ».

Catégorie : Analyse combinatoire

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Arrangement Avec Répétition de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Arrangement avec repetition — Arrangement avec répétition Un arrangement avec répétition en mathématiques, se produit lorsque nous rangeons dans un certain ordre k objets, choisis parmi n objets discernables, chaque objet pouvant être répété, nous pouvons représenter les… … Wikipédia en Français
Arrangement avec répétition — Un arrangement avec répétition en mathématiques, se produit lorsque nous rangeons dans un certain ordre k objets, choisis parmi n objets discernables, chaque objet pouvant être répété, nous pouvons représenter les différents rangements par des k… … Wikipédia en Français
Arrangement (Mathématiques) — Arrangement Pour les articles homonymes, voir Arrangement (homonymie). La notion d arrangement est utilisée en probabilités, et notamment pour les dénombrements en analyse combinatoire. En mathématiques, lorsque nous choisissons k objets parmi n… … Wikipédia en Français
Arrangement (mathematiques) — Arrangement Pour les articles homonymes, voir Arrangement (homonymie). La notion d arrangement est utilisée en probabilités, et notamment pour les dénombrements en analyse combinatoire. En mathématiques, lorsque nous choisissons k objets parmi n… … Wikipédia en Français
Arrangement (mathématiques) — Arrangement Pour les articles homonymes, voir Arrangement (homonymie). La notion d arrangement est utilisée en probabilités, et notamment pour les dénombrements en analyse combinatoire. En mathématiques, lorsque nous choisissons k objets parmi n… … Wikipédia en Français
Arrangement — Pour les articles homonymes, voir Arrangement (homonymie). La notion d arrangement est utilisée en probabilités, et notamment pour les dénombrements en analyse combinatoire. En mathématiques, lorsque nous choisissons k objets parmi n objets et… … Wikipédia en Français
arrangement — [ arɑ̃ʒmɑ̃ ] n. m. • XIIIe; de arranger ♦ Action d arranger; son résultat. 1 ♦ Action de disposer dans un certain ordre; la disposition qui en résulte. ⇒ disposition; assemblage, constitution, organisation. Arrangement d une maison, d un mobilier … Encyclopédie Universelle
Arranger — Arrangement Pour les articles homonymes, voir Arrangement (homonymie). La notion d arrangement est utilisée en probabilités, et notamment pour les dénombrements en analyse combinatoire. En mathématiques, lorsque nous choisissons k objets parmi n… … Wikipédia en Français
Analyse combinatoire — Combinatoire Pour les articles homonymes, voir combinatoire (homonymie). Une planche de l encyclopédie de Diderot et d … Wikipédia en Français
Combinatoire — Pour les articles homonymes, voir combinatoire (homonymie). Une planche de l encyclopédie de Diderot et d Alembert illustrant l article « Carreleur » … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Arrangement Avec Répétition