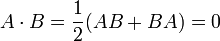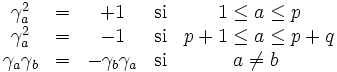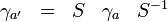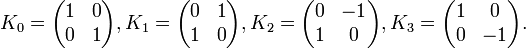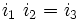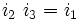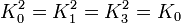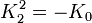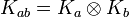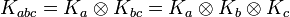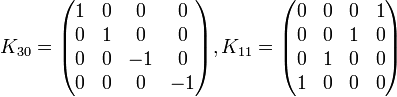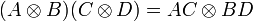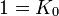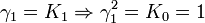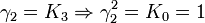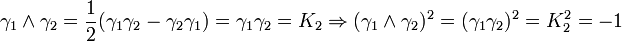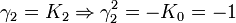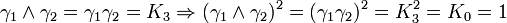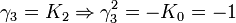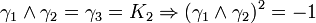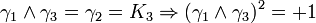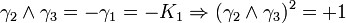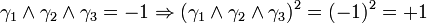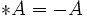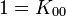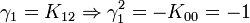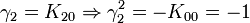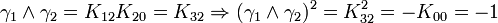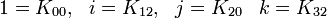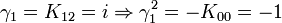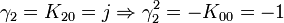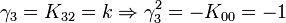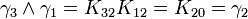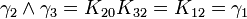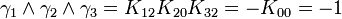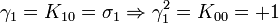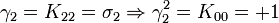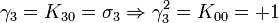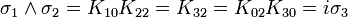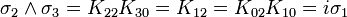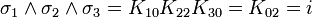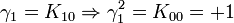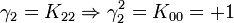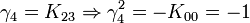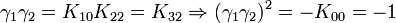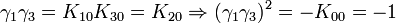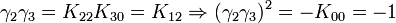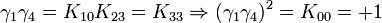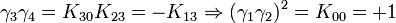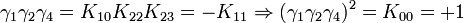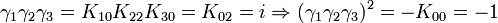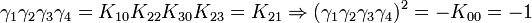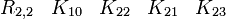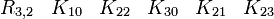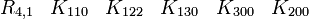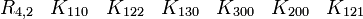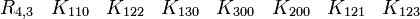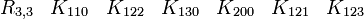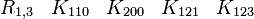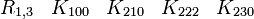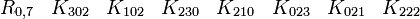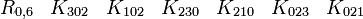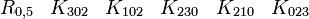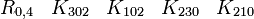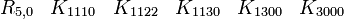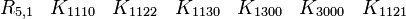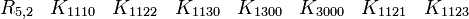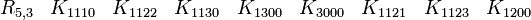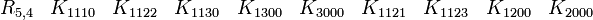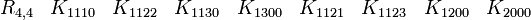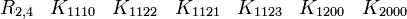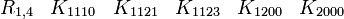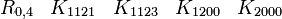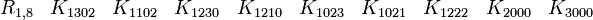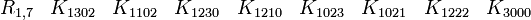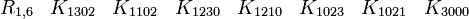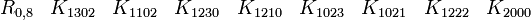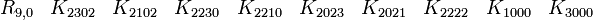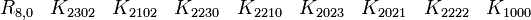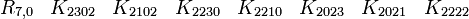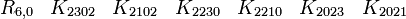Représentation des algèbres de clifford

Représentation des algèbres de Clifford

En mathématiques, les représentations des algèbres de Clifford sont aussi connues sous le nom modules de Clifford. En général, une algèbre de Clifford C est une algèbre centrale simple sur une certaine extension de corps L d'un corps K sur lequel la forme quadratique Q définissant C est définie.

La théorie algébrique des modules de Clifford a été mise au point par M. F. Atiyah, R. Bott et A. Shapiro dans l'article Clifford Modules (Topology 3 (Suppl. 1) (1964), 3–38).

Sommaire

1 Représentations matricielles des algèbres de Clifford réelles
2 Intermezzo : le système K pour nommer les matrices
3 L'algèbre de Clifford réelle R_2,0
4 L'algèbre de Clifford réelle R_1,1
5 L'algèbre de Clifford R_2,1
6 L'algèbre de Clifford R_0,2
7 L'algèbre de Clifford R_0,3
8 L'algèbre de Clifford R_3,0
9 L'algèbre de Clifford réelle R_3,1
10 Autres représentations avec les matrices réelles 4x4
11 Représentations avec les matrices réelles 8x8
12 Représentations avec les matrices réelles 16x16

Représentations matricielles des algèbres de Clifford réelles

Nous aurons besoin d'étudier les matrices anticommutatives (AB = -BA) les vecteurs orthogonaux anticommutent dans les algèbres de Clifford.

$A \cdot B = \frac{1}{2}( AB + BA ) = 0$

Pour l'algèbre de Clifford réelle 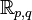$\mathbb{R}_{p,q}\,$ , nous avons besoin de p + q matrices mutuellement anticommutatives, dont p ont pour carré +1 et q ont pour carré - 1.

$\begin{matrix} \gamma_a^2 &=& +1 &\mbox{si} &1 \le a \le p \\ \gamma_a^2 &=& -1 &\mbox{si} &p+1 \le a \le p+q\\ \gamma_a \gamma_b &=& -\gamma_b \gamma_a &\mbox{si} &a \ne b \ \\ \end{matrix}$

Une telle base de matrices gamma n'est pas unique. On peut toujours obtenir un autre ensemble de matrices gamma satisfaisant la même algèbre de Clifford par une transformation de similarité.

$\begin{matrix} \gamma_{a'} &=& S &\gamma_{a } &S^{-1} \end{matrix}$

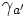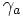où S est une matrice non-singulière. Les ensembles $\gamma_{a'}\,$ et $\gamma_{a}\,$ appartiennent à la même classe d'équivalence.

Intermezzo : le système K pour nommer les matrices

Nous présentons d'abord une méthode élégante pour nommer les matrices $2^n \times 2^n\,$

$K_0 = \begin{pmatrix} 1&0\\0&1 \end{pmatrix}, K_1 = \begin{pmatrix} 0&1\\1&0 \end{pmatrix}, K_2 = \begin{pmatrix} 0&-1\\1&0 \end{pmatrix}, K_3 = \begin{pmatrix} 1&0\\0&-1 \end{pmatrix}.$

À noter que K₀ est la matrice identité. Les noms ont été choisis de manière qu'il existe une règle simple pour se souvenir des produits :

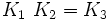
$K_1~K_2 = K_3\,$

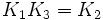
$K_1 K_3 = K_2\,$

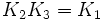
$K_2 K_3 = K_1\,$

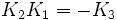
$K_2 K_1 = -K_3\,$

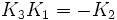
$K_3 K_1 = -K_2\,$

$K_3 K_2 = -K_1\,$ .

Incrémenter l'index donne un résultat positif. Décrémenter l'index donne un résultat négatif.

Attention ! Il n'existe PAS les mêmes relations valides pour la base standard des quaternions. Si vous vouliez nommer 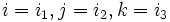$i = i_1, j = i_2, k = i_3\,$ vous obtiendriez

$i_1~i_2=i_3\,$

$i_2~i_3=i_1\,$

$i_3~i_1=i_2\,$

donc, la dernière règle est différente. Nous verrons plus tard que les quaternions purs i,j et k peuvent être représentés par K₁₂,K₂₀ et K₃₂

Remarquez que

$K_0^2 = K_1^2 = K_3^2 = K_0$

$K_2^2 = - K_0$

K₂ est la seule avec un carré négatif, donc elle peut être regardée comme la représentation la plus simple de i

Nous donnons un nom à tous les produits de Kronecker possibles (voir produit matriciel) :

$K_{ab} = K_{a} \otimes K_{b}$

$K_{abc} = K_{a} \otimes K_{bc}= K_{a} \otimes K_{b} \otimes K_{c}$

Quelques exemples

$K_{30} = \begin{pmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\ 0&0&0&-1 \end{pmatrix}, K_{11} = \begin{pmatrix} 0&0&0&1\\ 0&0&1&0\\ 0&1&0&0\\ 1&0&0&0 \end{pmatrix}$

Chaque index possède son niveau ( 2x2, 4x4, 8x8, 16x16, ...)

K₁₃ est une K₃ de niveau 2x2 et une K₁ de niveau 4x4. Avec cette notation, il est très simple de multiplier de grandes matrices puisque

$(A \otimes B)(C \otimes D) = AC \otimes BD$

Regardons un exemple

K₁₂₃ K₂₂₂ = K₃₀₁

niveau 8x8 1 fois 2 donne 3

niveau 4x4 2 fois 2 donne 0 mais souvenez-vous du signe moins

niveau 2x2 3 fois 2 donne 1 mais souvenez-vous du signe moins

(les deux signes moins s'annule donc le résultat est K₃₀₁ )

Nous pouvons maintenant démarrer la construction d'ensembles de matrices orthogonales mutuellement anticommutatives (voir matrice orthogonale), quelquefois appelées matrices de Dirac. Il est évident que deux de telles matrices anticommutent si elles anticommutent dans un nombre impair d'index (l'index o commute avec tous les autres indices).

K₁₃ par exemple anticommute avec

K₀₁,K₀₂,K₁₁,K₁₂,K₂₀,K₂₃,K₃₀,K₃₃

et commute avec

K₀₀,K₁₀,K₁₃,K₂₁,K₂₂,K₃₁,K₃₂.

Si l'index 2 apparaît un nombre pair de fois dans le nom alors le carré de la matrice est plus la matrice identité, appelons-la une Kplus

en voici des exemples : K₁, K₂₂, K₃₁₁, K₂₂₂₂

Si l'index 2 apparaît un nombre impair de fois dans le nom alors le carré de la matrice est moins la matrice identité, appelons-la une Kmoins

en voici des exemples : K₂, K₂₂₂, K₂₁₁, K₁₂₂₂

Nous avons maintenant une manière très simple de construction d'ensembles très larges de matrices anticommutatives.

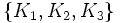
Démarrons avec un ensemble existant $\{K_1, K_2, K_3\}\,$

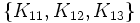
Insérons un nouvel index constant (par exemple un 1 dans la premère position) et vous obtenez $\{K_{11}, K_{12}, K_{13}\}\,$

Puis ajoutons deux matrices supplémentaires qui anticommutent dans le nouveau niveau et commutons dans l'ancien niveau (au moyen du zéro à l'index 0)

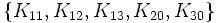
Donc, nous obtenons $\{K_{11}, K_{12}, K_{13}, K_{20}, K_{30}\}\,$

Autres exemples

{K₂₁, K₂₂, K₂₃, K₁₀, K₃₀}

{K₃₁, K₃₂, K₃₃, K₁₀, K₂₀}

{K₁₁₁, K₁₁₂, K₁₁₃, K₁₂₀, K₁₃₀, K₂₀₀, K₃₀₀}

{K₂₁₁, K₂₁₂, K₂₁₃, K₂₂₀, K₂₃₀, K₁₀₀, K₃₀₀}

{K₃₁₁, K₃₁₂, K₃₁₃, K₃₂₀, K₃₃₀, K₁₀₀, K₂₀₀}

Nous obtenons toujours un ensemble avec un nombre impair de matrices et il existe toujours une Kplus de plus qu'une Kmoins.

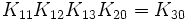
Chacune d'elles peut être écrite comme le produit de toutes les autres. Exemple : $K_{11} K_{12} K_{13} K_{20} = K_{30}\,$

L'algèbre de Clifford réelle R_2,0

p = 2 et q = 0, donc nous avons besoin de 2 Kplus comme base de vecteurs

catégorie 0 (le scalaire)

$\begin{matrix} 1 = K_0 \end{matrix}$

catégorie 1 (les vecteurs)

$\gamma_1 = K_1 \Rightarrow \gamma_1^2 = K_0 = 1$

$\gamma_2 = K_3 \Rightarrow \gamma_2^2 = K_0 = 1$

catégorie 2 (le pseudoscalaire)

$\gamma_1 \land \gamma_2 = \frac{1}{2}(\gamma_1 \gamma_2 - \gamma_2 \gamma_1 ) = \gamma_1 \gamma_2 = K_2 \Rightarrow (\gamma_1 \land \gamma_2)^2 = (\gamma_1 \gamma_2)^2 = K_2^2 = -1$

n = p + q = 2 et nous avons 2² = 4 éléments donc, c'est ce que I. Porteous appelle une algèbre de Clifford universelle.

L'algèbre de Clifford réelle R_1,1

p = 1 et q = 1 donc nous avons besoin d'une Kplus et d'une Kmoins comme base de vecteurs

Catégorie 0 (le scalaire)

$\begin{matrix} 1 = K_0 \end{matrix}$

catégorie 1 (les vecteurs)

$\gamma_1 = K_1 \Rightarrow \gamma_1^2 = K_0 = 1$

$\gamma_2 = K_2 \Rightarrow \gamma_2^2 = -K_0 = -1$

catégorie 2 (le pseudoscalaire)

$\gamma_1 \land \gamma_2 = \gamma_1 \gamma_2 = K_3 \Rightarrow (\gamma_1 \land \gamma_2)^2 = (\gamma_1 \gamma_2)^2 = K_3^2 = K_{0} = 1$

Ici encore, nous avons 2ⁿ éléments dans l'algèbre avec n = p+q donc elle est encore une algèbre de Clifford universelle.

L'algèbre de Clifford R_2,1

p = 2 et q = 1 donc 2 Kplus et 1 Kmoins pour base de vecteurs

catégorie 0 (le scalaire)

$\begin{matrix} 1 = K_0 \end{matrix}$

catégorie 1 (les vecteurs)

$\gamma_1 = K_1 \Rightarrow \gamma_1^2 = K_0 = 1$

$\gamma_2 = K_3 \Rightarrow \gamma_2^2 = K_0 = 1$

$\gamma_3 = K_2 \Rightarrow \gamma_3^2 = -K_0 = -1$

La signature est ( + + - )

catégorie 2 (les bivecteurs)

$\gamma_1 \land \gamma_2 = \gamma_3 = K_2 \Rightarrow (\gamma_1 \land \gamma_2)^2 = -1$

$\gamma_1 \land \gamma_3 = \gamma_2 = K_3 \Rightarrow (\gamma_1 \land \gamma_3)^2 = +1$

$\gamma_2 \land \gamma_3 = -\gamma_1 = -K_1 \Rightarrow (\gamma_2 \land \gamma_3)^2 = +1$

catégorie 3 (le pseudoscalaire)

$\gamma_1 \land \gamma_2 \land \gamma_3 = -1 \Rightarrow (\gamma_1 \land \gamma_2 \land \gamma_3)^2 = (-1)^2 = +1$

Ceci est le premier exemple d'une algèbre de Clifford non-universelle puisque p+q = 3 et nous avons seulement 2² éléments et non 2³. La raison est très simple, chaque matrice est utilisée deux fois, une fois comme vecteur et une fois comme bivecteur. Et le pseudoscalaire est réel, comme le scalaire.

(Le dual de Hodge de chaque élément est simplement le négatif de l'original)

$*A = -A\,$

L'algèbre de Clifford R_0,2

Ici p = 0 et q = 2 donc nous avons besoin de matrices Kmoins anticommutatives pour base de vecteurs. Ceci n'est pas possible avec des matrices réelles 2 x 2 donc nous avons besoin d'utiliser des matrices 4 x 4, et il existe beaucoup de possibilités. Cette algèbre est isomorphe avec l'anneau $\mathbb{H}\,$ des quaternions.

catégorie 0 (le scalaire)

$\begin{matrix} 1 = K_{00} \end{matrix}$

catégorie 1 (les vecteurs)

$\gamma_1 = K_{12} \Rightarrow \gamma_1^2 = -K_{00} = -1$

$\gamma_2 = K_{20} \Rightarrow \gamma_2^2 = -K_{00} = -1$

La signature est (- -)

catégorie 2 (le pseudoscalaire)

$\gamma_1 \land \gamma_2 = K_{12}K_{20} = K_{32} \Rightarrow (\gamma_1 \land \gamma_2)^2 = K_{32}^2 = -K_{00} = -1$

L'isomorphisme avec les quaternions est comme suit :

1 est scalaire, i et j sont les vecteurs et k = ij est le pseudoscalaire.

Un nombre de Clifford est une combinaison linéaire de quatre éléments 1, i, j et k

$\begin{matrix} 1 = K_{00}, &i = K_{12}, &j = K_{20} &k = K_{32} \end{matrix}$

L'utilisation de k comme pseudoscalaire ( i x j ) est un peu étrange mais sonne parfaitement.

L'algèbre de Clifford R_0,3

p = 0 et q = 3 donc nous avons besoin de 3 matrices Kmoins comme base de vecteurs, ceci est la manière usuelle de travail avec les quaternions i, j et k sont maintenant des base de vecteurs et ijk = -1 est le pseudoscalaire. Cette algèbre est de nouveau isomorphe avec $\mathbb{H}\,$ (les quaternions)

catégorie 0 (le scalaire)

$\begin{matrix} 1 = K_0 \end{matrix}$

catégorie 1 (les vecteurs)

$\gamma_1 = K_{12} = i \Rightarrow \gamma_1^2 = -K_{00} = -1$

$\gamma_2 = K_{20} = j \Rightarrow \gamma_2^2 = -K_{00} = -1$

$\gamma_3 = K_{32} = k \Rightarrow \gamma_3^2 = -K_{00} = -1$

La signature est ( - - - )

catégorie 2 (les bivecteurs)

$\gamma_1 \land \gamma_2 = K_{12} K_{20} = K_{32} = \gamma_3$

$\gamma_3 \land \gamma_1 = K_{32} K_{12} = K_{20} = \gamma_2$

$\gamma_2 \land \gamma_3 = K_{20} K_{32} = K_{12} = \gamma_1$

catégorie 3 (le pseudoscalaire)

$\gamma_1 \land \gamma_2 \and \gamma_3 = K_{12} K_{20} K_{32} = -K_{00} = -1$

Un nombre de Clifford est ici, de nouveau, une combinaison linéaire de 4 éléments 1 i j et k. L'usage de -1 comme pseudoscalaire (ijk) est comme nous l'avons employé, mais il fait de cette algèbre un nouvel exemple d'algèbre de Clifford non-universelle, puisque p + q = 3 et nous avons seulement 2² éléments.

L'algèbre de Clifford R_3,0

Ceci est la célèbre algèbre de Pauli, si vous pensez à K₀₂ pour i et K₀₀ pour 1. Nous avons trois Kplus pour base de vecteurs.

catégorie 0 (le scalaire)

$\begin{matrix} 1 = K_0 \end{matrix}$

catégorie 1 (les vecteurs)

$\gamma_1 = K_{10} = \sigma_1 \Rightarrow \gamma_1^2 = K_{00} = +1$

$\gamma_2 = K_{22} = \sigma_2 \Rightarrow \gamma_2^2 = K_{00} = +1$

$\gamma_3 = K_{30} = \sigma_3 \Rightarrow \gamma_3^2 = K_{00} = +1$

La signature est ( + + + )

catégorie 2 (les bivecteurs)

$\sigma_1 \land \sigma_2 = K_{10} K_{22} = K_{32} = K_{02} K_{30}= i \sigma_3$

$\sigma_3 \land \sigma_1 = K_{30} K_{10} = -K_{20} = K_{02}K_{22} = i \sigma_2$

$\sigma_2 \land \sigma_3 = K_{22} K_{30} = K_{12} = K_{02} K_{10} = i \sigma_1$

catégorie 3 (le pseudoscalaire)

$\sigma_1 \land \sigma_2 \and \sigma_3 = K_{10} K_{22} K_{30} = K_{02} = i$

Donc i est le pseudoscalaire et les équations pour les bivecteurs signifient en fait que chaque bivecteur est le dual de Hodge de l'un des vecteurs qui n'est pas une partie du bivecteur.

L'algèbre de Clifford réelle R_3,1

Ceci est pour moi l'algèbre de Clifford la plus intéressante parce qu'elle permet la construction des équations ressemblant aux équations de Dirac sans nombres complexes. Majorana l'a découverte. Par conséquent, les spineurs réels sont appelés les spineurs de Majorana. L'algèbre est aussi connue sous le nom d'algèbre de Majorana. Elle se sert de toutes les 16 matrices réelles 4 x 4. Les quatre bases de vecteurs sont en fait les trois matrices de Pauli (Kplus) completées d'une quatrième matrice antihermitienne (Kmin). La signature est ( + + + - ). Voir la convention de signe. Pour la signature ( + - - - ) ou ( - - - + ) souvent utilisée en physique, vous avez besoin de matrices complexes 4 x 4 ou matrices réelles 8 x 8 parce que vous ne pouvez pas former 3 matrices anticommutatives Kmoins 4 x 4. Voir R_1,3 pour différentes représentations.

catégorie 0 (le scalaire)

$\begin{matrix} 1 = K_0 \end{matrix}$

catégorie 1 (les vecteurs)

$\gamma_1 = K_{10} \Rightarrow \gamma_1^2 = K_{00} = +1$

$\gamma_2 = K_{22} \Rightarrow \gamma_2^2 = K_{00} = +1$

$\gamma_3 = K_{30} \Rightarrow \gamma_3^2 = K_{00} = +1$

$\gamma_4 = K_{23} \Rightarrow \gamma_4^2 = -K_{00} = -1$

La signature est ( + + + - )

catégorie 2 (les bivecteurs, trois rotations et trois accélérateurs)

$\gamma_1\gamma_2 = K_{10}K_{22} = K_{32} \Rightarrow (\gamma_1\gamma_2)^2 = -K_{00}= -1$

$\gamma_1\gamma_3 = K_{10}K_{30} = K_{20} \Rightarrow (\gamma_1\gamma_3)^2 = -K_{00}= -1$

$\gamma_2\gamma_3 = K_{22}K_{30} = K_{12} \Rightarrow (\gamma_2\gamma_3)^2 = -K_{00}= -1$

$\gamma_1\gamma_4 = K_{10}K_{23} = K_{33} \Rightarrow (\gamma_1\gamma_4)^2 = K_{00}= +1$

$\gamma_2\gamma_4 = K_{22}K_{23} = -K_{01} \Rightarrow (\gamma_1\gamma_2)^2 = K_{00}= +1$

$\gamma_3\gamma_4 = K_{30}K_{23} = -K_{13} \Rightarrow (\gamma_1\gamma_2)^2 = K_{00}= +1$

catégorie 3 (les pseudovecteurs, les duaux de Hodge des vecteurs)

$\gamma_2\gamma_3\gamma_4 = K_{22}K_{30}K_{23} = K_{31} \Rightarrow (\gamma_2\gamma_3\gamma_4)^2 = K_{00} = +1$

$\gamma_1\gamma_3\gamma_4 = K_{10}K_{30}K_{23} = -K_{03} \Rightarrow (\gamma_1\gamma_3\gamma_4)^2 = K_{00} = +1$

$\gamma_1\gamma_2\gamma_4 = K_{10}K_{22}K_{23} = -K_{11} \Rightarrow (\gamma_1\gamma_2\gamma_4)^2 = K_{00} = +1$

$\gamma_1\gamma_2\gamma_3 = K_{10}K_{22}K_{30} = K_{02} = i \Rightarrow (\gamma_1\gamma_2\gamma_3)^2 = -K_{00} = -1$

la dernière est le pseudoscalaire dans R_3,0

catégorie 4 (le pseudoscalaire)

$\gamma_1\gamma_2\gamma_3\gamma_4 = K_{10}K_{22}K_{30}K_{23} = K_{21} \Rightarrow (\gamma_1\gamma_2\gamma_3\gamma_4)^2 = -K_{00} = -1$

Autres représentations avec les matrices réelles 4x4

$\begin{matrix} R_{2,2} &K_{10} &K_{22} &K_{21} &K_{23} \end{matrix}$

$\begin{matrix} R_{3,2} &K_{10} &K_{22} &K_{30} &K_{21} &K_{23} \end{matrix}$

Représentations avec les matrices réelles 8x8

$\begin{matrix} R_{4,0} &K_{110} &K_{122} &K_{130} &K_{300} \end{matrix}$

$\begin{matrix} R_{4,1} &K_{110} &K_{122} &K_{130} &K_{300} &K_{200} \end{matrix}$

$\begin{matrix} R_{4,2} &K_{110} &K_{122} &K_{130} &K_{300} &K_{200} &K_{121} \end{matrix}$

$\begin{matrix} R_{4,3} &K_{110} &K_{122} &K_{130} &K_{300} &K_{200} &K_{121} &K_{123} \end{matrix}$

$\begin{matrix} R_{3,3} &K_{110} &K_{122} &K_{130} &K_{200} &K_{121} &K_{123} \end{matrix}$

$\begin{matrix} R_{2,3} &K_{110} &K_{122} &K_{200} &K_{121} &K_{123} \end{matrix}$

$\begin{matrix} R_{1,3} &K_{110} &K_{200} &K_{121} &K_{123} \end{matrix}$

Cette dernière est très importante en physique puisqu'elle est l'algèbre de Clifford la plus utilisée pour le travail dans l'espace-temps de Minkowski. La signature est ( + - - - ). Voir convention de signe. Les représentations les plus utilisées sont

$\begin{matrix} R_{1,3} &K_{100} &K_{210} &K_{222} &K_{230} \end{matrix}$

En s'intéressant aux matrices réelles 8 x 8, on peut former 7 matrices Kmoins anticommutatives. Ils forment un ensemble de bases pour l'algèbre de Clifford réelle non-universelle R_0,7

$\begin{matrix} R_{0,7} &K_{302} &K_{102} &K_{230} &K_{210} &K_{023} &K_{021} &K_{222} \end{matrix}$

$\begin{matrix} R_{0,6} &K_{302} &K_{102} &K_{230} &K_{210} &K_{023} &K_{021} \end{matrix}$

$\begin{matrix} R_{0,5} &K_{302} &K_{102} &K_{230} &K_{210} &K_{023} \end{matrix}$

$\begin{matrix} R_{0,4} &K_{302} &K_{102} &K_{230} &K_{210} \end{matrix}$

(Pour R_0,3, nous avons montré qu'une seule a besoin de matrices réelles 4x4)

Représentations avec les matrices réelles 16x16

$\begin{matrix} R_{5,0} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{3000} \end{matrix}$

$\begin{matrix} R_{5,1} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{3000}&K_{1121} \end{matrix}$

$\begin{matrix} R_{5,2} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{3000}&K_{1121} &K_{1123} \end{matrix}$

$\begin{matrix} R_{5,3} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{3000}&K_{1121} &K_{1123} &K_{1200} \end{matrix}$

$\begin{matrix} R_{5,4} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{3000}&K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}$

$\begin{matrix} R_{4,4} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}$

$\begin{matrix} R_{3,4} &K_{1110} &K_{1122} &K_{1130} &K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}$

$\begin{matrix} R_{2,4} &K_{1110} &K_{1122} &K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}$

$\begin{matrix} R_{1,4} &K_{1110} &K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}$

$\begin{matrix} R_{0,4} &K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}$

$\begin{matrix} R_{1,8} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{1023} &K_{1021} &K_{1222} &K_{2000} &K_{3000} \end{matrix}$

$\begin{matrix} R_{1,7} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{1023} &K_{1021} &K_{1222} &K_{3000} \end{matrix}$

$\begin{matrix} R_{1,6} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{1023} &K_{1021} &K_{3000} \end{matrix}$

$\begin{matrix} R_{1,5} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{1023} &K_{3000} \end{matrix}$

$\begin{matrix} R_{1,4} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{3000} \end{matrix}$

R_1,3 a besoin seulement de matrices réelle 4x4

$\begin{matrix} R_{0,8} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{1023} &K_{1021} &K_{1222} &K_{2000} \end{matrix}$

R_0,7 a besoin seulement de matrices réelles 8x8

$\begin{matrix} R_{9,0} &K_{2302} &K_{2102} &K_{2230} &K_{2210} &K_{2023} &K_{2021} &K_{2222} &K_{1000} &K_{3000} \end{matrix}$

$\begin{matrix} R_{8,0} &K_{2302} &K_{2102} &K_{2230} &K_{2210} &K_{2023} &K_{2021} &K_{2222} &K_{1000} \end{matrix}$

$\begin{matrix} R_{7,0} &K_{2302} &K_{2102} &K_{2230} &K_{2210} &K_{2023} &K_{2021} &K_{2222} \end{matrix}$

$\begin{matrix} R_{6,0} &K_{2302} &K_{2102} &K_{2230} &K_{2210} &K_{2023} &K_{2021} \end{matrix}$

R_5,0 a besoin seulement de matrices réelles 8x8

Portail des mathématiques

Ce document provient de « Repr%C3%A9sentation des alg%C3%A8bres de Clifford ».

Catégorie : Théorie des représentations

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Représentation des algèbres de clifford de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Representation des algebres de Clifford — Représentation des algèbres de Clifford En mathématiques, les représentations des algèbres de Clifford sont aussi connues sous le nom modules de Clifford. En général, une algèbre de Clifford C est une algèbre centrale simple sur une certaine… … Wikipédia en Français
Représentation des algèbres de Clifford — En mathématiques, les représentations des algèbres de Clifford sont aussi connues sous le nom modules de Clifford. En général, une algèbre de Clifford C est une algèbre centrale simple sur une certaine extension de corps L d un corps K sur lequel … Wikipédia en Français
Classification des algèbres de Clifford — En mathématiques, en particulier dans la théorie des formes quadratiques non dégénérées sur les espaces vectoriels réels et complexes, les algèbres de Clifford de dimension finie ont été complètement classées. Dans chaque cas, l algèbre de… … Wikipédia en Français
Algebre de Clifford — Algèbre de Clifford En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des… … Wikipédia en Français
Algèbre De Clifford — En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des généralisations possibles des… … Wikipédia en Français
Algèbre de Clifford du plan euclidien) — Algèbre de Clifford En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des… … Wikipédia en Français
Algèbre de clifford — En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des généralisations possibles des… … Wikipédia en Français
Algèbre de Clifford — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Représentation des algèbres de clifford