Reduction de matrice

Sommaire 1 Rappels 1.1 Endomorphisme et représentation matricielle 1.2 Matrices et endomorphismes 2 Diagonalisation 3 Trigonalisation 4 Applications de la réduction d'endomorphisme

Rappels

Endomorphisme et représentation matricielle

S'agissant des endomorphismes d'espace vectoriel de dimension finie, il est courant et très pratique de les représenter matriciellement. La matrice d'un tel endomorphisme dépend alors de la base choisie pour le représenter. La théorie de réduction des endomorphismes en dimension finie consiste à chercher une base dans laquelle cette matrice est la plus simple possible : dans le meilleur des cas, une matrice diagonale (dont seuls les éléments diagonaux peuvent ne pas être nuls, il s'agit alors d'une diagonalisation), sinon une matrice triangulaire supérieure (dont seuls les éléments diagonaux et sur-diagonaux peuvent ne pas être nuls, il s'agit alors de trigonalisation).

Matrices et endomorphismes

Étant donné un espace vectoriel E de dimension n, rapporté à une base β, à tout endomorphisme de E, on peut associer une matrice carrée d'ordre n représentant u dans cette base. On l'appelle la matrice de u dans β. Ses vecteurs colonne sont les images dans β de chacun des vecteurs ordonnés de cette même base.

Réciproquement, étant données une matrice A carrée d'ordre n, et une base β de E, il existe un unique endomorphisme dont la matrice dans cette base soit A.

Par ailleurs, étant donnée une matrice A carrée d'ordre n sur un corps , on appelle endomorphisme canoniquement associé à A l'endomorphisme de 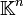dont la matrice dans la base canonique de 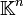est A. C'est l'application linéaire .

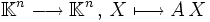Diagonalisation

Une matrice carrée A est dite diagonalisable si et seulement si l'endomorphisme qui lui est canoniquement associé est diagonalisable : elle est alors semblable à une matrice diagonale, c’est-à-dire s'il existe une matrice P inversible telle que la matrice P ^{− 1}AP soit diagonale.

Trigonalisation

Lorsqu'un endomorphisme n'est pas diagonalisable, on peut se demander s'il existe une base par rapport à laquelle sa matrice est triangulaire.

Définition :

Un endomorphisme u de E est dit trigonalisable s'il existe une base de E par rapport à laquelle la matrice de u est triangulaire supérieure. Une matrice carrée A est dite trigonalisable si elle est semblable à une matrice triangulaire supérieure, c'est-à-dire s'il existe une matrice inversible P telle que P ^{− 1}AP soit triangulaire.

Supposons la matrice A, à coefficients dans un corps K, trigonalisable et semblable à la matrice triangulaire T. Les valeurs propres de T sont les éléments de sa diagonale, ce sont donc des éléments du corps K. Comme A et T sont semblables, elles ont les mêmes valeurs propres et de ce fait les valeurs propres de A appartiennent toutes au corps K. Par conséquent, pour que la matrice A soit trigonalisable, il est nécessaire que les racines de son polynôme caractéristique soient dans le corps K. Cette condition est toujours vérifiée lorsque K est le corps des nombres complexes.

On démontre que cette condition est aussi suffisante pour assurer la trigonalisabilité.

Proposition 3 :

Soit u un endomorphisme d'un K-espace vectoriel de dimension finie. Les conditions suivantes sont équivalentes :

1. u est trigonalisable
2. Le polynôme caractéristique de u est scindé dans K[X], c'est-à-dire qu'il s'écrit sous forme du produit de polynômes de degré 1 à coefficients dans le corps K.

Applications de la réduction d'endomorphisme

• Calcul des puissances d'une matrice carrée.

• Exponentielle d'une matrice.