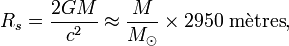Rayon De Schwarzchild

Le rayon de Schwarzschild est défini comme le rayon critique prévu par la géométrie de Schwarzschild, en deçà duquel rien ne peut s'échapper : si une étoile ou tout autre objet atteint un rayon égal ou inférieur à son rayon de Schwarzschild (qui dépend de sa masse, cf ci-dessous), alors elle devient un trou noir, et tout objet s'approchant à une distance de celui-ci inférieure au rayon de Schwarzschild ne pourra s'en échapper. Le terme est utilisé en physique et en astronomie pour donner un ordre de grandeur de la taille caractéristique à laquelle des effets de relativité générale deviennent nécessaires pour la description d'objets d'une masse donnée. Les seuls objets qui ne sont pas des trous noirs et dont la taille est du même ordre que leur rayon de Schwartzschild sont les étoiles à neutrons (ou pulsars), ainsi, curieusement, que l'univers observable en son entier.

Le terme doit son origine à l'astrophysicien allemand Karl Schwarzschild, découvreur en 1916 de la première solution exacte aux équations d'Einstein, qui s'est avéré ultérieurement décrire un trou noir (voir métrique de Schwarzschild). Incidemment, Schwarzschild signifie en allemand bouclier noir, terme particulièrement adapté au concept de trou noir.

Les distortions de l'espace-temps au voisinage d'un trou noir rendent le concept de distance un peu subtil. Le terme de rayon de Schwarzschild se réfère en fait au rayon que l'on associerait à un objet d'une circonférence donnée en géométrie euclidienne : il n'est pas possible de mesurer le rayon d'un trou noir en le traversant (puisque rien ne peut s'en échapper), il est par contre possible d'en mesurer la circonférence en faisant le tour sans y pénétrer.

Ce rayon est de ce fait appelé horizon du trou noir (on ne peut voir ce qu'il s'y passe à l'intérieur). Le rayon de Schwarzschild est proportionnel à la masse de celui-ci, et se détermine par la relation suivante (qui est une conséquence de la définition de la vitesse de libération appliquée à la vitesse la lumière) :

où G est la constante de gravitation, M la masse du trou noir, 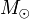la masse du Soleil et c la vitesse de la lumière. La valeur exacte de ce rayon est modifiée dans le cas où l'objet considéré possède une charge électrique non nulle ou un moment cinétique. En pratique, seul le moment cinétique joue un rôle, la charge électrique étant négligeable dans toutes les configurations où des trous noirs sont produits, mais dans tous les cas, le rayon de Schwarzschild exprimé en kilomètres est de l'ordre de trois fois la masse de l'objet considéré exprimée en masses solaires.

Du fait de la petitesse de la quantité 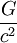dans les unités usuelles, le rayon de Schwarzschild d'un objet astrophysique est très petit : pour la masse de la Terre, il est de seulement 9 millimètres. Puisque le rayon moyen de la Terre est d'environ 6 370 kilomètres, la Terre devrait être comprimée jusqu'à atteindre 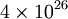fois sa densité actuelle avant de pouvoir s'effondrer en un trou noir : il n'est pas facile de former des trous noirs de faible masse. Un trou noir stellaire typique a un rayon qui se compte en dizaines de kilomètres. Pour un objet de la masse du soleil, le rayon de Schwarzschild est d'environ 3 kilomètres, ce qui est bien inférieur aux 700 000kilomètres du rayon actuel du Soleil. Le rayon de Schwarzschild du Soleil est également sensiblement plus petit que le rayon que le Soleil aura après avoir épuisé son carburant nucléaire, soit plusieurs milliers de kilomètres quand il sera devenu une naine blanche. Des étoiles plus massives peuvent cependant s'effondrer en trous noirs à la fin de leur vie. Dans le cas d'un trou noir supermassif, du genre de ceux que l'on trouve au centre de nombreuses galaxies, le trou noir a une masse de quelques millions à plusieurs milliards de masses solaires, pour un rayon de plusieurs millions à plusieurs milliards de kilomètres, soit moins que la taille de l'orbite de Neptune. Cette petite taille rend difficile la détection directe des trous noirs, faute d'une résolution angulaire suffisante. Il reste cependant possible de pouvoir imager directement le trou noir central de notre Galaxie par des méthodes d'interférométrie à très longue base (VLBI). D'éventuels trous noirs primordiaux, de très faible masse (quelques milliards de tonnes) pourraient éventuellement exister. De tels trous noirs seraient de taille microscopique, et ne seraient détectables que par leur rayonnement, résultant du phénomène d'évaporation des trous noirs.

Voir aussi

• Relativité générale
• Trou noir
• Géométrie de Schwarzschild
• Trou noir stellaire
• Trou noir supermassif
• Trou noir primordial

• Portail de l’astronomie