- Quatrième dimension
-
La quatrième dimension est le temps des 3 dimensions.
Sommaire
En physique
La première mention de la quatrième dimension apparaît chez d'Alembert dans l'Encyclopédie, article Dimension : « Un homme d’esprit de ma connaissance croit qu’on pourrait cependant regarder la durée comme une quatrième dimension » «Mais c'est aussi une sensation. »
En géométrie
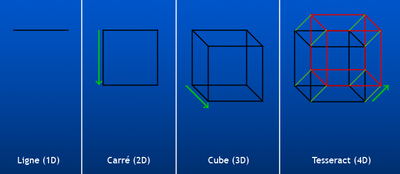 Un point translaté donne un segment, un segment translaté donne un carré, un carré translaté donne un cube, un cube translaté donne un tesseract, etc.
Un point translaté donne un segment, un segment translaté donne un carré, un carré translaté donne un cube, un cube translaté donne un tesseract, etc.
Les concepts de plans et d'espaces euclidiens peuvent être encore élargis à d'autres dimensions au dessus. On passe d'un univers à 3 dimensions (espace) à un univers à 4 dimensions de la même façon qu'on passe d'un univers à 2 dimensions (plan) à un univers à 3 dimensions (espace) et de la même façon qu'on passe d'un univers à 1 dimension (droite) à un univers à 2 dimensions (plan)... Le repère orthonormé d'un univers à N dimensions est alors formé de N axes gradués, tous perpendiculaires entre eux les uns les autres en un même point appelé origine. Par exemple, un tesseract est un objet à quatre dimensions spatiales : son intersection avec un espace peut être un cube de la même façon que l'intersection d'un cube avec un plan peut donner un carré. Le tesseract standard en 4-espace euclidien est donné par l'enveloppe convexe des points (±1, ±1, ±1, ±1). Le tesseract peut être développé en huit cubes, comme le cube peut être développé en six carrés. Le développement d'un polyèdre est appelé un patron. Il existe 261 patrons distincts du tesseract.
Les géométries à N dimensions et les géométries non-euclidiennes sont deux branches séparées de la géométrie. Une confusion s'est établie dans la littérature populaire à propos de ces deux géométries. Parce que la géométrie euclidienne était à trois dimensions, on en concluait que les géométries non-euclidiennes comportaient nécessairement des dimensions supérieures.
- Notion de 4e dimension chez Poincaré
"L'espace moteur aurait autant de dimensions que nous avons de muscles" : cette affirmation de Poincaré dans La Science et l'Hypothèse est la marque de distinction la plus claire entre les deux sortes d'espace qu'il envisage : l'espace géométrique et l'espace représentatif.
- Les hypercubes en architecture informatique.
- En informatique le terme hypercube fait référence à un type précis d'ordinateur parallèle, dont les processeurs, ou les éléments de calcul (PEs), sont interconnectés de la même manière que les sommets d'un hypercube.
Ainsi, un ordinateur hypercube n-dimensionnel a 2n PEs, chacun directement connecté à n autres PEs.
En physique d'Einstein (relativité)
- La quatrième dimension représente le temps qui fait partie du référentiel espace-temps.
En spiritualisme
Quatrième dimension ou monde en quatre dimensions, un nouveau concept apporté par Bedri Ruhselman, un spiritualiste turc.
En art, littérature
- Comment le concept mathématique de quatrième dimension a été popularisé dans l'art (cubisme), la littérature (science fiction, vulgarisation, ésotérisme) : 4ème dimension (art).
- Gorck's Land, trilogie sur la quatrième dimension de Kevin Bokeili, éditions Quatrième Zone (le nom de est une composition issue de quatrième dimension et de twilight zone).
- Terre-616 de l'univers Marvel Comics
- Univers DC de DC Comics
En cinéma, télévision,
La Quatrième Dimension est le titre français:
- d'une série télévisée de science-fiction : La Quatrième Dimension
- d'un film à sketches de 1983 : La Quatrième Dimension, hommage de Steven Spielberg, John Landis, Joe Dante et George Miller à la série télévisée du même nom.
En fait, ce titre est dû à un épisode très célèbre appelé "Little Girl Lost" ou "Petite Fille Perdue" en français. Cet épisode relate la disparition d'une petite fille dans une dimension spatiale supérieure : un monde à quatre dimensions.
En informatique
- 4e Dimension ou 4D est un système de gestion de base de données (SGBD)
- Cinema 4D est un logiciel de modélisation 3D
Liens externes
- MagicCube 4D Un analogue quadridimensionnel du traditionnel Rubik's Cube.
- 4DNav Un petit outil de visualisation d'un espace en 4 dimensions.
Notes et références
Wikimedia Foundation. 2010.
