- Quadrature du carré
-
Un carré dont les côtés sont égaux à une unité de longueur multipliée par un nombre entier est appelé un carré entier. Le problème de la quadrature du carré consiste à paver un carré donné avec de tels carrés.
La quadrature du carré est une tâche triviale sans conditions supplémentaires fixées. La restriction la plus étudiée est la quadrature « parfaite » du carré, où tous les carrés contenus sont de tailles différentes (voir ci-dessous).
D'autres conditions peuvent conduire à des résultats intéressants. L'une d'elle est la quadrature du carré sans jonction de bord (c’est-à-dire la jonction complète de bords de même taille n'est pas autorisée) et la quadrature du carré sans contact (c’est-à-dire l'interdiction à deux pièces de même taille de se toucher) (voir pavage).
Sommaire
Quadrature parfaite du carré
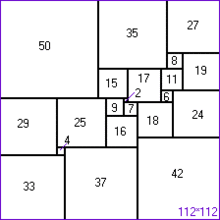
Une quadrature « parfaite » du carré est telle qu'un carré est constitué de carrés plus petits chacun de taille différente. Le nom fut attribué par analogie humoristique avec la quadrature du cercle.
Il a été enregistré en premier qu'elle a été étudiée par R. L. Brooks, C. A. B. Smith, A. H. Stone, et W. T. Tutte, à l'université de Cambridge.
Pour ce faire, ils ont transformé le pavage du carré en un circuit électrique équivalent, en considérant les carrés comme des résistors qui étaient connectés à leurs voisins à leur limite supérieure et inférieure, puis ils appliquèrent les lois de Kirchhoff concernant les circuits électriques et les techniques de décomposition de circuit à ce circuit.
La première quadrature parfaite du carré fut trouvée par Roland Sprague en 1939.
Si nous prenons une pièce du pavage et que nous l'élargissons jusqu'à ce que le plus petit carré ait maintenant la taille du carré S dont nous sommes partis, alors nous pouvons voir que nous obtenons à partir de ceci un pavage du plan avec des carrés entiers, chacun ayant une taille différente.
C'est encore un problème non-résolu que de savoir si le plan peut être pavé avec un ensemble de carrés entiers tels que chacun d'eux ait une taille différente utilisant un nombre naturel et utilisé une seule fois.
Martin Gardner a écrit un long article à propos de l'histoire de la quadrature du carré.
Quadrature simple du carré
Une quadrature « simple » du carré est celle dont aucun sous-ensemble de carrés ne forme un rectangle. La plus petite quadrature parfaite simple du carré fut découverte par A. J. W. Duijvestin en utilisant une recherche par ordinateur. Son pavage utilise 21 carrés, et a été démontré comme étant minimal.
Le quilt de Mrs. Perkins
Lorsque la contrainte que tous les carrés soient de tailles différentes est levée, le problème de la quadrature du carré résultant est souvent appelé le problème du « quilt de Mrs. Perkins ».
Lectures
- Brooks, R. L.; Smith, C. A. B.; Stone, A. H.; and Tutte, W. T. The Dissection of Rectangles into Squares, Duke Math. J. 7, 312-340, 1940
- Martin Gardner, « Squaring the square, » in The 2nd Scientific American Book of Mathematical Puzzles and Diversions.
- C. J. Bouwkamp and A. J. W. Duijvestijn, Catalogue of Simple Perfect Squared Squares of Orders 21 Through 25, Eindhoven Univ. Technology, Dept. of Math., Report 92-WSK-03, Nov. 1992.
- C.J.Bouwkamp and A.J.W.Duijvestijn, Album of Simple Perfect Squared Squares of order 26, Eindhoven University of Technology, Faculty of Mathematics and Computing Science, EUT Report 94-WSK-02, December 1994.
Voir aussi
Liens externes
- Quadratures parfaites du carré :
- Quadrature du carré sans jonction :
Wikimedia Foundation. 2010.