Période propre

La fréquence propre d'un système est la fréquence à laquelle oscille ce système lorsqu'il est en évolution libre, c'est-à-dire sans force excitatrice extérieure ni forces dissipatives (frottements ou résistances par exemple). Cette notion est fondamentale pour comprendre les phénomènes d'oscillation et de résonance. Elle est largement utilisée dans tous les domaines de la physique et trouve des applications concrètes dans la conception des horloges, des instruments de musique, mais aussi en génie civil pour éviter les résonances sur les grandes structures comme les ponts.

De la fréquence propre sont déduites la période propre et la pulsation propre. Si on appelle f₀ la fréquence propre on a respectivement :

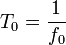et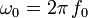

Sommaire 1 Mécanique 2 Électronique 3 Synthèse 4 Notes et références 5 Voir aussi 5.1 Articles connexes 5.2 Liens externes 5.3 Bibliographie

Mécanique

Considérons un pendule constitué d'un balancier pouvant osciller librement autour d'un axe horizontal. Dans le cas de l'oscillateur idéal, il n'y a pas de frottement. On peut modéliser le pendule par une masse ponctuelle suspendue au bout d'un fil inextensible et de masse nulle (pendule simple). Les équations auxquelles on aboutit sont identiques dans leur forme mathématique et ce modèle est suffisant pour comprendre le principe d'une horloge à balancier. Si l'on étudie le mouvement du balancier dans le cas du pendule réel, le théorème du moment cinétique donne :

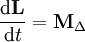
• L : moment cinétique du balancier
• M_Δ : moment des forces par rapport à l'axe Δ

avec

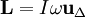
où I est le moment d'inertie du solide par rapport à l'axe Δ, ω, sa vitesse angulaire de rotation et 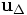est le vecteur unitaire colinéaire à Δ.

Le moment des forces par rapport à l'axe Δ, en l'absence de frottements, se ramène au moment du poids du balancier, on a :

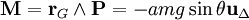
On obtient alors l'équation

,

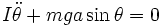d'où 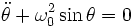avec .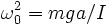

L'étude d'un point matériel suspendu au bout d'un fil de longueur l donnant

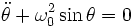
avec 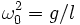, on obtient une équation qui est mathématiquement identique à celle que l'on obtient dans le cas du mouvement du balancier, justifiant ainsi de se ramener au cas d'une masse ponctuelle suspendue au bout d'un fil pour comprendre le principe des horloges à balancier.

Dans le cas idéal, on se limite aux petites oscillations du pendule au voisinage de sa position d'équilibre, soit 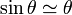, ce qui donne :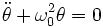

Électronique

L'exemple le plus courant est celui de la montre à quartz. Pour comprendre le principe d'une horloge à quartz, il faut étudier son composant essentiel : une lamelle de quartz placée entre deux électrodes. Une lamelle de quartz soumise à une compression mécanique voit apparaître une tension à ses bornes et vice-versa (voir piézoélectricité). Le quartz est équivalent à un circuit L, R, C₁ série (L, R et C₁ ne dépendent que des caractéristiques physiques du quartz) placé en parallèle avec une capacité C₂ qui correspond à la capacité créée par les deux électrodes qui enserrent le morceau de quartz. Dans le cas idéal, on suppose qu'il n'y a pas de perte d'énergie, c'est-à-dire que :

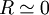
Le circuit « idéal » est alors un simple circuit L, C où la capacité C équivalente à C₁ et C₂ en série vérifie :

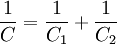
L'équation correspondant à cette situation s'écrit :

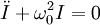
pour l'intensité et

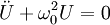
pour la tension aux bornes de L, C

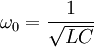
Synthèse

Les solutions des équations pour l'horloge à balancier aussi bien que pour l'horloge à quartz sont de la même forme :

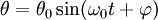
pour le pendule mécanique « idéal » et

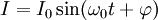
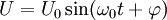
pour un circuit L, C sans perte énergétique.

La période est T = 2π / ω₀. La fréquence propre des oscillations du système ω₀ ne dépend pas de leur amplitude mais uniquement des caractéristiques de l'oscillateur (et de g dans le cas du pendule) :

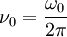
Notes et références

Voir aussi

Articles connexes

• Fréquence
• Onde
• Résonance magnétique nucléaire
• Signal périodique
• Série de Fourier
• Transformée de Fourier

Liens externes

Bibliographie

• Portail de la physique