- Prévisions économiques
-
Prévision économique
La Prévision économique est l'estimation, généralement par des méthodes économétriques, des valeurs actuelles ou futures de grandeurs économiques.
Elle est utilisée par exemple pour estimer l'évolution du PIB ou de l'inflation, et orienter les comportements d'investissement des entreprises ou la politique économique de la banque centrale et du gouvernement.
La prévision économique est toujours incertaine, et aux estimations des valeurs futures sont toujours associés des intervalles de confiance. L'incertitude sur les décisions politiques, les chocs économiques (et les réactions en chaîne qui en découlent) et l'ampleur des cycles économiques rend l'exercice de prévision périlleux. En économie ouverte, les changements dans un pays ont des conséquences sur l'activité économique des partenaires commerciaux.
Certaines variables, comme les taux de change, sont particulièrement difficiles à prévoir. Plusieurs auteurs ont ainsi relevé l'incapacité des experts à anticiper les variations importantes des cours du dollar et la sous-évaluation systématique des mouvements de toutes les grandeurs macro-économiques.
La science économique est une discipline qui a fort évolué depuis les années 1930. Les mécanismes de fonctionnement de l'économie sont à présent mieux compris que par le passé et la gamme des outils et des théories à la disposition des économistes s'est largement étendue. La prévision économique a connu également de nombreux développements. Il existe une diversité impressionnante de théories et de techniques qui tentent de répondre à la variété des tâches de prévision économique existant de par le monde. Les progrès de l’informatique ont joué un rôle prépondérant dans l’élargissement du spectre des méthodes de prévision. Étant donné la taille énorme prise par la discipline de la prévision économique, nous nous sommes restreints à mentionner certains de ses aspects dans cet article.
Sommaire
Quelques définitions
La prévision
Une prévision peut être définie comme un ensemble de probabilités associées à un ensemble d’événements futurs (Fischhoff, 1994). Cette prévision est basée sur un ensemble d'informations disponibles à l'instant t où elle a été effectuée. Cet ensemble noté Ωt (l'indice temporel t correspond à l'instant t) représente les données disponibles, les connaissances et les théories concernant le phénomène que l'on souhaite prévoir. La prévision au temps t d'horizon h de la variable Y, considérée comme une variable aléatoire, peut donc s'écrire (Granger et Newbold, 1977) sous la forme d'une fonction de distribution conditionnelle (à l'ensemble d'informations Ωt) :
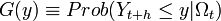
Prévision ponctuelle - Intervalle de confiance des prévisions
En ce qui concerne les variables numériques (les plus rencontrées en économie), il est plus fréquent que l'on se contente en pratique de fournir une valeur centrale des prévisions, comme la moyenne ou la médiane. On qualifie cette prévision de ponctuelle (point forecast en anglais) et on la note Ft,h. L'autre façon d'exprimer sa prévision est de donner un intervalle de confiance des prévisions (prediction interval) que l'on note
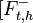 ,
, ![F_{t,h}^{+} ]](/pictures/frwiki/99/cabebe7d728dc98bfdb280a18ad54947.png) . Cela revient à révéler une information partielle sur la fonction de distribution attendue.
. Cela revient à révéler une information partielle sur la fonction de distribution attendue.Un exemple de prévision centrale: « La croissance du PIB sera de l'ordre de 2% en 2009 en France. » Un exemple d'intervalle de prévision: « Le taux de croissance du PIB variera sera compris entre 1,75 et 2,25% en France en 2009. » Dans la pratique, on rencontre des formes hybrides de prévision. Ainsi, un cas fréquent est l’évocation d'une borne supérieure des prévisions: « la croissance de l'activité économique ne devrait pas dépasser 2% en 2009. »
Dans ces différents exemples, aucune probabilité n'est associée à la prévision. Dans le cas contraire, on pourrait avoir : « Nous estimons à 95%, la probabilité que le taux de croissance du PIB en 2009 soit compris entre 1,75 et 2,25% en 2009. » Les raisons pour lesquelles on préfère communiquer ou publier uniquement la valeur centrale des prévisions dans la pratique ont été analysées notamment par Chatfield (1993).
Planification et anticipation
Le prévisionniste n'a en général pas de contrôle sur le phénomène qu'il essaye de prédire. Dans ce cas, on dit qu'il formule des anticipations. Il existe cependant quelques exceptions. Un entrepreneur qui veut connaître la valeur des ventes futures de sa société a un certain contrôle sur la variable à prédire, dans la mesure où il peut agir directement sur certains de ses déterminants (la politique de prix, le budget de publicité). On parle alors de planification. Formellement, si Ωt + h représente l'ensemble d'informations couvrant l'intervalle de temps [t,t + h], le planificateur possède le contrôle sur un sous-ensemble
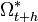 de Ωt + h. Il existe évidemment des cas intermédiaires entre l'anticipation et la planification, notamment lorsque le prévisionniste peut agir indirectement sur la variable prédite. Un exemple bien connu en économie est celui des "gourous", des "spécialistes". Par le simple fait d'émettre une prévision, ces "super-agents" peuvent influencer les agents économiques; lesquels vont adapter leur comportement et par conséquence agir sur la variable en question.
de Ωt + h. Il existe évidemment des cas intermédiaires entre l'anticipation et la planification, notamment lorsque le prévisionniste peut agir indirectement sur la variable prédite. Un exemple bien connu en économie est celui des "gourous", des "spécialistes". Par le simple fait d'émettre une prévision, ces "super-agents" peuvent influencer les agents économiques; lesquels vont adapter leur comportement et par conséquence agir sur la variable en question.Horizon de prévision
L'horizon de prévision (noté h) varie de l'immédiat au long terme. Cette notion dépend du domaine étudié ainsi que de l'intervalle de temps s'écoulant entre deux observations successives. Pour des données industrielles mensuelles, le court terme exprime en général un horizon allant de 3 à 15 mois. Pour des données macroéconomiques annuelles, le court terme est utilisé pour les prévisions d'horizon 1 et 2 ans (que l'on appelle aussi prévisions conjoncturelles). En finance, pour des données journalières ou disponibles en temps réel, le court terme évoque plutôt l'heure suivante ou le lendemain.
Fonction de perte, de coût
Cette notion exprime le coût, les pertes engendrées par les erreurs de prévision. Elle prend son sens lorsque la prévision est exprimée sous la forme d'une valeur centrale Ft,h. Formellement, l'erreur de prévision d'horizon h est notée et,h et définie ainsi :
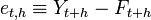 . Le fait que les erreurs de prévision soient non nulles entraîne des coûts pour les agents économiques qui ont utilisé ces prévisions (firmes, ménage, état) pour prendre des décisions qui s'avèrent non optimales. La fonction de coût notée C(et,h) peut prendre différentes formes. Les plus connues étant les fonctions de coût quadratique et de valeur absolue.
. Le fait que les erreurs de prévision soient non nulles entraîne des coûts pour les agents économiques qui ont utilisé ces prévisions (firmes, ménage, état) pour prendre des décisions qui s'avèrent non optimales. La fonction de coût notée C(et,h) peut prendre différentes formes. Les plus connues étant les fonctions de coût quadratique et de valeur absolue.Il existe cependant d'autres fonctions de coût, dont les fonctions de coût asymétriques qui sont fréquentes dans la réalité (Granger et Newbold, 1977, citent notamment quelques exemples).
L'objectif du prévisionniste est en général d’être crédible, c’est-à-dire de minimiser la fonction de coût de son auditoire (l'ensemble des consommateurs de ses prévisions). S'il est rémunéré par un agent particulier (par exemple une firme), le prévisionniste professionnel doit se baser sur la fonction de coût personnelle de cet agent. Dans de nombreux cas, le prévisionniste et le consommateur de la prévision sont une même personne (une firme ou un ménage qui souhaite estimer ses revenus futurs). Par contre, s'il n'existe pas de lien direct (un contrat de travail ou un engagement moral) entre le prévisionniste et les consommateurs de sa prévision, il peut y avoir un décalage entre la fonction de coût des agents et la fonction de coût implicite du prévisionniste.
L'évolution des techniques de la prévision économique
Les racines de la prévision économique
Les premières approches structurées de la prévision économique datent du siècle dernier. Ainsi, Juglar a attiré l'attention sur la périodicité apparente des crises économiques et sur la possibilité de les prévoir (voir cycle économique). Un certain nombre de développements en statistiques concernant les phénomènes saisonniers observés pour des séries chronologiques de nature climatique ont lieu à la même époque et sont envisagés pour les séries économiques.
Au début du XXe siècle, les travaux du comité de Harvard connaîtront leur heure de gloire. Ils aboutissent à un système de prévision automatique se basant sur l'ordre de succession de courbes relatives aux sphères financière, réelle et monétaire. La première version de ce système fut mise au point en 1917. Dans l'optique de ce système, il n'y a aucune recherche des causes des fluctuations des séries étudiées; il y a un rejet de tout élément personnel et subjectif pouvant intervenir dans l'élaboration des prévisions.
Le succès rencontré par les travaux de la Harvard School fut à l'origine de la création d'instituts de conjoncture dans un certain nombre de pays industrialisés. La Grande Dépression porta cependant un coup fatal à la prévision automatique et permit d'accorder plus de crédits à des théories, des méthodes jusque là embryonnaires.
Déjà, avant la crise des années trente, les travaux de Moore (1923), Fisher (1925) et Slutsky (1927) dénonçaient le caractère déterministe des cycles économiques. Les travaux de Yule (1927) conférèrent une dimension nouvelle au problème de la prévision statistique: la distinction entre processus déterministe et stochastique étant établie. Dans cette lignée les travaux de Wold, qui introduit en 1938 les modèles ARMA (autoregressive moving average), forment la base de l'actuelle discipline de l’analyse des séries temporelles.
Toujours dans les années 1930, la régression multiple est utilisée à des fins prévisionnelles. En ce qui concerne les prévisions macroéconomiques, l'impulsion décisive est donnée par la conjonction des travaux de Keynes (1936) et du développement en matière de comptabilité nationale. Ces progrès débouchent sur la mise au point par Tinbergen (1939) dans les années 1930 du premier modèle économétrique.
Évolution depuis l'après guerre: la diversification des applications et des techniques
Après guerre, la continuité des travaux de Tinbergen sera assurée notamment par Klein (1950), qui fournit les premières simulations prévisionnelles.
Dans la période de l'après guerre à nos jours, une conjonction de nombreux facteurs va faire avancer l'art de la prévision économique, qu'elle concerne les phénomènes micro, méso ou macroéconomiques et va faire augmenter de façon explosive le nombre des techniques, des procédures de la prévision économique.
Les progrès dans l'informatique ont une part fondamentale dans ces développements. Tout d'abord, les ordinateurs ont permis d'élargir considérablement le nombre de données économiques publiées, de par la réduction des coûts de leur stockage et de leur traitement. D'autre part, leur faculté de calcul rapide et de traitement de volumes d'information de plus en plus grand, ont permis à de nombreuses disciplines de se développer. La statistique et l'économétrie figurent parmi ces disciplines.
En se développant, l'économétrie — qui constitue en quelque sorte un outil de laboratoire de la science économique — a permis de faire progresser cette dernière. Un cercle vertueux apparaissant, les progrès de la science économique nécessitant de nouvelles techniques économétriques et ainsi de suite. Les développements des techniques économétriques applicables à la prévision sont très nombreux: citons notamment les modèles d'équations simultanées (Zellner, 1962), la causalité (Granger, 1969) les modèles à correction d'erreur et la cointégration (Engle et Granger, 1987).
Les méthodes de prévision "statistiques" se sont également développées. Citons chronologiquement les développements du lissage exponentiel (Brown, 1962), la décomposition saisonnière (Shiskin et Eisenpress, 1957), l'analyse des séries temporelles (Box et Jenkins, 1970, première édition), les modèles non linéaires (Engle, 1982) et les méthodes bayésiennes (Zellner, 1970). En outre, de nouvelles techniques d'inférence statistique ont vu le jour (inférence exacte, méthode du va et vient ou 'bootstraping', Méthode de Monte-Carlo, etc.).
En parallèle, des progrès plus liés aux aspects organisationnels des firmes ont été effectués (voir Makridakis et al., 1983). Ainsi, dans les années 1950, de nouvelles disciplines sont apparues comme la recherche opérationnelle et les techniques de gestion (management science) et permirent d'améliorer la prise de décision au sein d'une entreprise.
Les progrès continus de l'informatique depuis 1950 et leur diffusion dans les entreprises ont permis l'émergence de la prévision assistée par informatique d'émerger et de s'imposer. Des logiciels spécialisés (comme par exemple SAS ou R) ont fait leur apparition.
L'ensemble de ces progrès ainsi que l'augmentation des phénomènes économiques que l'on souhaite prévoir ont abouti à une diversité impressionnante de techniques de prévision. Nous tentons dans la section suivante de classifier ces techniques suivant le critère choisi habituellement: l'ensemble d'information requis (
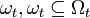 ) par chaque méthode pour établir la prévision.
) par chaque méthode pour établir la prévision.Classification des techniques de prévision
Les méthodes sont regroupées en catégories, de la façon suivante:
- les approches basées sur le jugement, ou informelles
- les méthodes extrapolatives ou univariées
- les méthodes explicatives ou causales
- les méthodes systémiques et économétriques
Afin de pouvoir mieux comprendre la portée de ces méthodes sont mentionnés un exemple typique d'application de chaque méthode ainsi que l'horizon (ou les horizons) de prévision recommandé pour l'utilisation de chaque méthode (TCT: très court terme, CT: court terme, MT: Moyen terme, LT: long terme). Les méthodes peuvent être combinées. C'est d'autant plus pertinent de recourir aux combinaisons lorsque les méthodes sont jugées complémentaires et qu'il existe une grande incertitude sur le meilleur modèle à employer.
Les méthodes informelles
Les méthodes informelles ou de jugement (judgemental) sont très répandues dans le monde de l'entreprise. Plus généralement, elles sont particulièrement utiles dans toutes les applications caractérisées par une information quantitative déficiente (données non mesurables, peu fiables ou trop peu nombreuses) alors qu'un certain nombre de connaissances, d'informations qualitatives sont disponibles.
Principales méthodes informelles:
- Réunions d'experts
- Planification, politique de prix (évolution des ventes, du budget promotionnel), horizon: CT,MT, LT
- Confrontation des forces des ventes (sales force composite). Exemple : évolution des ventes pour l'ensemble d'une firme qui vend différents produits). horizon: CT ou MT
- Développements de scénarios. Ex: déchets produits par une firme, une région. horizon: MT ou LT
- Approche Delphi. Variables qualitatives, planification, politique de prix. horizon: CT MT LT
Les méthodes extrapolatives
Les méthodes extrapolatives utilisent les observations quantitatives du passé de la variable pour prédire son futur. Autrement dit: ωt = (Y0,...,Yt − 2,Yt − 1,Yt).
Elles sont utilisées principalement pour la prévision à court terme ainsi que lorsque des variables explicatives ne sont pas disponibles ou manquent de fiabilité. Elles permettent notamment de modéliser l’inertie propre à de nombreuses variables économiques. Des informations contextuelles concernant le phénomène étudié permettent en général d'améliorer l'application des méthodes extrapolatives.
Principales méthodes extrapolatives ou univariées:
- Prévision naïve. Phénomène incertain à prévoir (ex: prévision du cours d'une action), horizon : TCT
- Lissage exponentiel (simple, double, adaptatif, amorti, etc.). Séries courtes, de nature industrielle, microéconomique, de fréquence mensuelle ou trimestrielle (ex: production du secteur textile au cours des trois prochains mois), horizon : TCT / CT
- Courbes de croissance(régression linéaire,logistique, Gompertz, etc.). Séries annuelles, peu cycliques, assez régulières(ex: cycle de vie d'un produit). horizon: MT / LT
- Décomposition saisonnière (moyennes mobiles, X-11, X-11 ARIMA, X-12, etc.). Séries trimestrielles et surtout mensuelles qui présentent d'importantes fluctuations saisonnières(ex: consommation de biens alimentaires). horizon : CT
- Modélisation ARIMA (méthodologie de Box et Jenkins, etc.). Séries longues(ex: production industrielle trimestrielle). horizon: CT
- Décomposition spectrale (composantes non observées). Séries longues(ex: production industrielle trimestrielle). horizon: CT
- Modèles ARFIMA, mémoire longue. Séries très longues, séries annuelles(ex: évolution des prix pétroliers). horizon: MT / LT
- Modèles stochastiques non linéaires (à seuil, bilinéaire, à erreurs GARCH, à coefficients dépendant du temps, etc.). Séries longues, de nature financière (données journalières, en temps réel), séries économiques volatiles (variables monétaires)(ex: taux de change $/DM, taux d’intérêt). horizon: TCT / CT
- Modèles dynamiques linéaires bayésiens. Séries longues et pour laquelle on dispose des informations à priori (ex: ventes de la société). horizon: CT
- Méthodes chartistes (basées sur l’analyse de courbes). Données financières (ex: cours des actions). horizon: CT
Les méthodes explicatives
Les méthodes explicatives utilisent les valeurs passées d’une ou de k variables, y compris, éventuellement, la variable étudiée Y (appelée variable dépendante).
Formellement, ωt = [(Y0,...,Yt − 2,Yt − 1,Y0),(X1,0,...,X1,t − 2,X1,t − 1,X1,t)...(Xi,0,...,Xi,t − 2,Xi,t − 1,Xi,t)...(XK,0,...,XK,t − 2,XK,t − 1,XK,t)], où
![i \in[1, 2, .., K]](/pictures/frwiki/100/d73ef93f0aa82097ac14cf07e8be0ec9.png) , avec K est le nombre total de variables explicatives.
, avec K est le nombre total de variables explicatives.Ceci implique que la qualité des prévisions obtenues à l’aide de ces méthodes dépend entre autres de la qualité de prévision ou d’estimation des variables explicatives sur l’horizon de prévision. Cette catégorie de méthodes est particulièrement recommandée lorsqu'il existe des variables explicatives dont les observations sont disponibles plus rapidement que la variable dépendante. Pour la prévision conjoncturelle, on se base notamment sur ce qu'on appelle des indicateurs avancés ("leading indicators") de l'économie.
Principales méthodes explicatives:
- Régression multiple. Planification (ex: prévision des ventes en fonction de la politique de prix et du budget consacré à la promotion). horizon: CT / MT / LT
- Modèles de fonction de transfert. Séries longues (ex: prévision de l'activité en fonction d'indicateurs avancés). Prév. CT MT
- Modèles à correction d’erreurs, modèles VAR, VARMA. Séries longues et variables économiques qui interagissent toutes entre elles (ex: variables macro-économiques, consommation privée et produit intérieur brut). horizon: CT / MT
- Modèles dynamiques linéaires bayésiens. Séries longues pour lesquelles on dispose des informations à priori (ex: ventes de la société). horizon: CT
Les méthodes systémiques
Les méthodes systémiques tendent à considérer le système économique dans sa totalité. Elles utilisent les relations et les interactions possibles entre de nombreuses variables.
Formellement, ωt = [(Y0,...,Yt − 2,Yt − 1,Y0),(X1,0,...,X1,t − 2,X1,t − 1,X1,t)...(Xi,0,...,Xi,t − 2,Xi,t − 1,Xi,t)...(XK,0,...,XK,t − 2,XK,t − 1,XK,t)], où
![i \in[1, 2, .., K]](/pictures/frwiki/100/d73ef93f0aa82097ac14cf07e8be0ec9.png) , avec K est le nombre total de variables explicatives.
, avec K est le nombre total de variables explicatives.Ces méthodes sont utilisées pour la modélisation macro-économique et méso-économique principalement. Elles servent d’instrument de simulation (planification, politique budgétaire, politique monétaire) et de prévision à moyen et long terme.
- Equations simultanées (double moindres carrés, triple moindres carrés, etc.). Quand la distinction entre variables exogènes et endogènes est possible (ex: offre et demande en fonction du prix d'un bien). horizon: CT / MT / LT
- Modèles macroéconomiques. Variables macroéconomiques pour lesquelles il existe un cadre théorique bien défini (équilibre général). horizon: LT
Autres considérations
Certaines informations n'ont pas été reprises ici. On aurait ainsi pu spécifier si la prévision est calculée à partir d'un modèle ou une formule, quand cette information est disponible, bien entendu. Plus généralement, on aurait également pu classer les méthodes de prévision en méthodes paramétriques, non paramétriques et semi paramétriques.
Certaines méthodes plus récentes, comme les réseaux de neurones et les algorithmes d'apprentissage et de classification, ne sont pas reprises dans cet article.
Voir aussi
Sources
- PASTEELS, Jean-Michel (1997). Extrait de la thèse de doctorat; "L'expertise dans la prévision à court terme de variables économiques: contributions méthodologiques et empiriques". Université Libre de Bruxelles.
Bibliographie
ARMSTRONG, J. S. (1985). Long-Range Forecasting. Wiley-Interscience, New York
BATES, J.M. et GRANGER, C.W.J. (1969). The combination of forecasts, Operations Research Quarterly, 20, 319-325.
BUNN, D. et WRIGHT, G. (1991). Interaction of judgemental and statistical forecasting methods: issues and analysis, Management Science, 37, 501-517.
CARNOT, N. et TISSOT B. (2002). La prévision économique, Economica, Paris, 483 p.
CHATFIELD, C. (1993). Calculating interval forecasts, Journal of Business & Economic Statistics, 11, 121-135.
CLEMENTS, M.P. et HENDRY, D.F. (1996). Economic Forecasting, Cambridge University Press, Cambridge.
FISCHHOFF, B. (1994). What forecasts (seem to) mean, International Journal of Forecasting, 10, 387-403.
FISHER, I. (1925). Booms and Depressions. Some first principles. Wiley, New York.
GOODWIN, P. (1993). Improving judgmental time series forecasting: A review of the guidance provided by research, International Journal of Forecasting, 9, 147-161.
GRANGER, C. W. J. et NEWBOLD, P. (1977). Forecasting Economic Time Series. Academic Press, New York (1re édition).
GRANGER, C.W.J. (1996). Can we improve the perceived quality of economic forecasts ?, Journal of Applied Econometrics, 11, 455-473.
KLEIN, L.R. (1950). Economic Fluctuations in the United States 1921-1941. Wiley, New York
MAHMOUD, E., DEROECK, R., BROWN, R. et RICE, G. (1992). Bridging the gap between theory and practice in forecasting, International Journal of Forecasting, 8, 251-267.
MAKRIDAKIS, S., WHEELWRIGHT, S. S. et McGEE, V. E. (1983). Forecasting: Methods and Applications. Wiley, New York (2e édition).
MELARD, G. (1990). Méthodes de prévision à court terme. Editions de l'Université de Bruxelles, Bruxelles et Editions Ellipses, Paris.
MENTZER, J.T. et KAHN, K.B. (1995). Forecasting technique familiarity, satisfaction, usage, and application, Journal of Forecasting, 14, 465-476.
MOORE, H.L. (1923). Generating Economic Cycles. New York.
MORGENSTERN, O. (1963). On the Accuracy of Economic Observations. Princeton University Press, Princeton.
SHISKIN, J. et EISENPRESS, H. (1957). Seasonal adjustments by electronic computer methods, Journal of the American Statistical Association, 52, 415-449.
MUTH, J.F. (1960) Optimal properties of exponentially weighted forecasts, Journal of the American Statistical Association, 55, 299-306.
SLUTSKY, E. (1937). The summation of random causes as the source of cyclic processes, Econometrica, 5, 105-146.
THEIL, H. (1966). Applied Economic Forecasting. North-Holland, Amsterdam.
TINBERGEN, J. (1939). Statistical testing of business cycle theories II. Business cycles in the United States of America 1919-1932. League of Nations, Geneva.
WEISS, A.A (1996). Estimating time series models using the relevant cost function, Journal of Applied Econometrics, 11, 539-560.
Notes et références de l'article
Articles connexes
- Modèle (économie) (les modèles économiques utilisés)
- Exemples d'utilisation de la prévision économique
Liens externes
- Portail de l’économie
- Portail des probabilités et des statistiques
Catégories : Théories et modèles économiques | Statistiques
Wikimedia Foundation. 2010.
