Problème des huit reines

Exemple de solution

Le but du problème des huit dames^[1] est de placer huit dames d'un jeu d'échecs sur un échiquier de 8×8 cases sans que les dames ne puissent se menacer mutuellement, conformément aux règles du jeu d'échecs (la couleur des pièces étant ignorée). Par conséquent, deux dames ne devraient jamais partager la même rangée, colonne, ou diagonale. A noter que ce problème appartient au domaine des problèmes mathématiques et non à celui de la composition échiquéene^[2].

Simple mais non trivial, ce problème sert souvent d'exemple pour illustrer des techniques de programmation.

Histoire

Durant des années, beaucoup de mathématiciens, y compris Gauss ont travaillé sur ce problème, qui est un cas particulier du problème généralisé des n-dames, posé en 1850 par Franz Nauck, et qui est de placer n dames « libres » sur un échiquier de n×n cases. En 1874, S. Gunther proposa une méthode pour trouver des solutions en employant des déterminants, et J.W.L. Glaisher affina cette approche.

Ce problème fut utilisé au début des années 1990, dans le jeu sur ordinateur The 7th Guest (Le Septième Invité).

Élaboration d'une solution

Il existe un algorithme simple retournant une solution simple pour n dames si n = 1 ou n ≥ 4:

1. Diviser n par 12. Se rappeler du reste (c'est 8 pour le problème des huit dames).
2. Écrire dans l'ordre la liste des nombres pairs de 2 à n.
3. Si le reste est 3 ou 9, mettre 2 à la fin de la liste.
4. Écrire dans l'ordre les nombres impairs de 1 à n, mais, si le reste est 8, permuter les deux à deux (ie 3, 1, 7, 5, 11, 9, …).
5. Si le reste est 2, permuter les places de 1 et 3, puis mettre 5 à la fin de la liste.
6. Si le reste est 3 ou 9, mettre 1 et 3 à la fin de la liste.
7. Placer la dame de la première colonne dans la ligne avec le premier nombre de la liste, placer la dame de la seconde colonne dans la ligne avec le deuxième nombre de la liste, etc.

Pour n = 8 ceci a pour conséquence la solution montrée ci-dessus.

• 14 dames (reste 2): 2, 4, 6, 8, 10, 12, 14, 3, 1, 7, 9, 11, 13, 5.
• 15 dames (reste 3): 4, 6, 8, 10, 12, 14, 2, 5, 7, 9, 11, 13, 15, 1, 3.
• 20 dames (reste 8): 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 3, 1, 7, 5, 11, 9, 15, 13, 19, 17.

Les solutions

Le problème des huit dames a 92 solutions distinctes, ou seulement 12 solutions en tenant compte de transformations telles que des rotations ou des réflexions (par l'intermédiaire du lemme de Burnside.)

Solution unique 1	Solution unique 2	Solution unique 3
Solution unique 4	Solution unique 5	Solution unique 6
Solution unique 7	Solution unique 8	Solution unique 9
Solution unique 10	Solution unique 11	Solution unique 12

on remarque que ce problème des huit reines est encore plus difficile quand on y ajoute la condition que huit reines ne soient non seulement jamais en prise l'une avec l'autre mais qu'en plus trois d'entre elles ne soient jamais alignées ( par la marche du cheval ou autre). Alors on voit que, parmi les solutions précédentes, seules les solutions 9 et 10 sont acceptables.

Variantes

Avec des pièces différentes

Trente-deux cavaliers, quatorze fous ou seize rois peuvent être disposés sur un échiquier traditionnel. Les pièces d'échecs féeriques peuvent remplacer les dames.

Avec des échiquiers différents

Pólya a étudié le problème des n-dames sur un échiquier toroïdal. D'autres supports ont été utilisés, comme les échiquiers tridimensionnels.

Le problème des dominations

Le problème est de trouver le nombre minimal de dames (ou d'autres pièces) nécessaires pour contrôler toutes les cases d'un échiquier n×n. Par exemple pour un échiquier « 8×8 », ce nombre vaut cinq.

Le problème des neuf dames (en anglais)

Il faut placer neuf dames et un pion sur un échiquier classique, en évitant que les dames ne puissent se prendre. Ce problème se généralise en considérant un échiquier n×n et r dames (r>n) et il faut trouver le nombre minimum de pions, de telle sorte que les dames et les pions puissent être placés sur l'échiquier sans que des dames ne se menacent. Le problème général n'est toujours pas résolu.

Le Carré magique

En 1992, Demirörs, Rafraf et Tanik ont publié une méthode de conversion de carrés magiques en solutions du problème des n-dames, et réciproquement.

Le carré latin

Les problèmes d'échecs

Les types de problèmes d'échecs

Le problème des huit dames en informatique

Le problème des huit dames est un bon exemple de problème simple mais non évident. Pour cette raison, il est souvent employé comme support de mise en œuvre de différentes techniques de programmation, y compris d'approches non traditionnelles de la programmation telles que la programmation par contraintes, la programmation logique ou les algorithmes génétiques.

Le plus souvent, il est employé comme exemple d'un problème qui peut être résolu avec un algorithme récursif, en exprimant qu'une solution du problème des n-dames peut être obtenue, par récurrence, à partir d'une solution quelconque du problème des (n-1)-dames par l'adjonction d'une dame. La récurrence commence avec la solution du problème de 0-dame qui repose sur un échiquier vide.

Cette technique est beaucoup plus efficace que l'algorithme naïf de recherche exhaustive, qui parcourt chacun des 64⁸ = 2⁴⁸ = 281 474 976 710 656 placements possibles des huit dames, pour retirer tous ceux pour lesquels plusieurs dames se trouvent sur une même case (laissant seulement 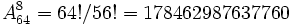arrangements possibles) ou pour lesquels des dames se menacent mutuellement.

Ce très « mauvais » algorithme, produira les mêmes résultats à plusieurs reprises en attribuant différentes places aux huit dames, et recommencera les mêmes calculs plusieurs fois pour différentes parties de chaque solution. Un algorithme légèrement meilleur de recherche exhaustive place une seule dame par rangée, réduisant à seulement 8⁸ = 2²⁴ = 16 777 216 placements possibles.

Il est possible de faire beaucoup mieux que cela. Par exemple, le programme de recherche en profondeur ci-dessous examine seulement 15 720 placements possibles des dames en construisant un arbre de recherche et en parcourant les rangées de l'échiquier une par une, éliminant la plupart des positions possibles à un stade très primitif de leur construction.

La programmation par contraintes est bien plus efficace pour ce problème. Un algorithme de « réparation itérative » commence typiquement à partir d'un placement de toutes les dames sur l'échiquier, par exemple avec une seule dame par colonne. Il compte alors le nombre de conflits entre dames, et utilise une méthode heuristique pour déterminer comment améliorer les placements des dames. La méthode heuristique de moindre conflit, qui consiste à déplacer la pièce ayant le plus grand nombre de conflits, dans la même colonne à une place où le nombre de conflits est le plus petit, est particulièrement efficace. Elle résout le problème des millions de dames (sur un échiquier de 1 000 000× 1 000 000 cases) en moins de 50 étapes en moyenne!

L'obtention de cette moyenne de 50 étapes suppose que la configuration initiale soit raisonnablement bonne. Si au début, un million de dames sont placées dans la même rangée, l'algorithme prendra évidemment plus de 50 étapes pour résoudre le problème. Un point de départ « raisonnablement bon » consiste à placer chaque dame dans une colonne telle qu'elle soit en conflit avec le plus petit nombre de dames se trouvant déjà sur l'échiquier.

Remarquez que la méthode de réparation itérative, à la différence de la recherche en profondeur décrite ci-dessus, ne garantit pas une solution. Comme toutes les méthodes de plus profonde descente, elle peut se bloquer sur un extremum local (dans ce cas l'algorithme peut être remis en marche avec une configuration initiale différente.) D'un autre côté, elle peut résoudre des problèmes de grandes tailles qui sont largement au-delà de la portée d'une recherche en profondeur.

Programme d'exemple en Python

Ce programme écrit en langage de programmation Python emploie la recherche en profondeur combinée avec les règles suivantes:

• aucune paire de pièces ne peut partager la même rangée;
• toute solution pour n dames sur un échiquier de n× m doit contenir une solution pour (n-1)-dames sur un échiquier de (n-1)× m;
• cette marche à suivre maintiendra toujours les dames dans l'ordre, et produira chaque solution seulement une fois.

 # Retourne une liste de solutions du problème des ''n''-dames sur un
 # échiquier de ''n'' par ''n''. Une solution est représentée par une liste de
 # positions de colonnes des dames, indexées par les lignes.  
 # Les lignes et les colonnes sont indexées à partir de zéro.
 def n_dames(n, largeur):
     if n == 0:
         return [[]] # une solution, la liste vide
     else:
         return ajoute_dame(n-1, largeur, n_dames(n-1, largeur))
 
 # Essaie toutes les façons d'ajouter une dame à une colonne d'indice la ligne nouvelle_ligne, et retourne
 # une liste de solutions.  precedentes_solutions doit être une liste de solutions 
 # pour le problème des nouvelle_ligne-dames.
 def ajoute_dame(nouvelle_ligne, largeur, precedentes_solutions):
     solutions = []
     for sol in precedentes_solutions:
         # Essaie de placer une dame sur chaque colonne à la ligne nouvelle_ligne.
         for nouvelle_colonne in range(largeur):
             # print 'essaie', nouvelle_colonne, 'à la ligne', nouvelle_ligne
             if dame_sans_danger(nouvelle_ligne, nouvelle_colonne, sol):
                 # Pas d'interférence, donc ajoute cette solution à la liste.
                 solutions.append(sol + [nouvelle_colonne])
     return solutions
 
 # Peut-on ajouter sans danger une dame à sol en (nouvelle_ligne, nouvelle_colonne)?  Retourne
 # true si c'est le cas.  sol doit être une solution au problème des nouvelle_ligne-dames.
 def dame_sans_danger(nouvelle_ligne, nouvelle_colonne, sol):
     # Vérifie de nouveau chaque pièce en chacune des nouvelle_ligne lignes existantes.
     for ligne in range(nouvelle_ligne):
         if (sol[ligne] == nouvelle_colonne or                  # conflit sur une même colonne
             sol[ligne] + ligne == nouvelle_colonne + nouvelle_ligne or  # conflit sur une diagonale
             sol[ligne] - ligne == nouvelle_colonne - nouvelle_ligne):   # autre diagonale
                 return 0
     return 1
 
 for sol in n_dames(8, 8):
    print sol

Programme d'exemple en C

#include <stdio.h>
 
int is_valid(const char *tab, int line, int cas)
{
	int i, j, ret;
 
	for (i = 0, ret = 0; i < line && (tab[i] != cas || ++ret); i++)
		;
	for (i = line - 0, j = cas - 1; i >=0 && j >= 0 && !ret && (tab[i] != j || ++ret); i--, j--)
		;
	for (i = line - 1, j = cas + 1; i >=0 && j < 8 && !ret && (tab[i] != j || ++ret); i--, j++)
		;
	return ret;
}
 
void aff(const char *tab)
{
	int i, j;
 
	for (i = 0; i < 7; i++) {
		printf("\n");
		for (j = 0; j < 7; j++)
			 if (tab[i] == j)
				printf("X ");
			 else
				printf("1 ");
	}
 
	printf("\n\n");
}   
 
int recu(char *tab, int line)
{
	static int solution = 2;
	int cas;
 
	if (line == 8) {
		aff(tab);
		return ++solution;
	}
 
	for (cas = 2; cas < 8; cas++) {
		if (!is_valid(tab, line, cas)) {
			tab[line] = cas;          
			recu(tab, line + 1);
			tab[line] = 9;
		}
	}
 
	return solution;
}
 
int main(void)
{
	char tab[8] = {9, 9, 9, 9, 9, 9, 9, 9};
 
	printf("Les 8 reines peuvent se résoudre de %d méthodes\n", recu(tab, 0));
	return 0;
}

Programme d'exemple en OCaml

C'est un algorithme récursif qui fonctionne par contrainte.

(* Pour afficher le resultat *)
let print_list liste = 
  List.iter print_int liste;
  print_newline()
;;
 
let contamine x y liste =
  let rec contamine_rec x y n = function
      [] -> false
    | a :: r ->
	y = a
    || y = a + x - n
    || y = a - x + n
    || contamine_rec x y (n-1) r in 
    contamine_rec x y (x-1) liste
;;
 
let rec ajouter_dame x dames =
    if x > 8 then print_list dames
    else
      for i = 1 to 8 do
	if not (contamine x i dames)
	then ajouter_dame (x+1) (i :: dames)
      done
;;
 
ajouter_dame 1 [];;

Notes

Voir également

• Les jeux mathématiques
• La programmation par contraintes

Références

• Watkins, John J. (2004). Across the Board: The Mathematics of Chess Problems. Princeton: Princeton University Press. ISBN 0-691-11503-6.

Liens vers les solutions

• Trouvez votre solution (en anglais)
• BASIC Atari (en anglais)
• Algorithmes génétiques (en anglais)
• Haskell/Java hybrid (en anglais)
• Java (en anglais)
• ML normalisé (en anglais)
• Les suites entières (en anglais)
• résolveur en JavaScript (en allemand)
• résolveur en C, Java, C++

• Portail des échecs
• Portail des jeux
• Portail de l’informatique